一番最初に学ぶべき機械学習モデル それは重回帰分析！！

こんにちは、nissyです。

本日は「データサイエンス初学者が一番最初に学ぶべき機械学習モデル」について紹介したいと思います。

結論としては重回帰分析1択です。

重回帰分析は非常に汎用性が高い分析手法であり、ビジネス・マーケティングなどさまざまな分野で活用されています。

化学実験のデータに対しても適用可能であり、特に複雑系である化学製品の分析を行う上では非常に重要な分析手法であると言えます。

今回は重回帰分析からどのような結果がアウトプットとして得られるのか、また重回帰分析を行うメリット、気をつけるべきこと等について説明していきます。

この記事では、scikit-learnでの重回帰分析の実装を想定して解説していきます。

回帰分析とは
1. 単回帰分析
2. 重回帰分析
Pythonで重回帰分析を実装
重回帰分析からさらにその先へ
まとめ

回帰分析とは

回帰分析とは機械学習における”教師あり学習”の一つです。

目的に応じたy=f(X)なるモデルを構築し、構築したモデルを使って未来に得られるデータの目的変数yを予測することに使えます。

機械学習モデルのことを目的変数yを説明する関数f(x)と考えて、「y=f(X)を構築する」と言ったりします。

単回帰分析

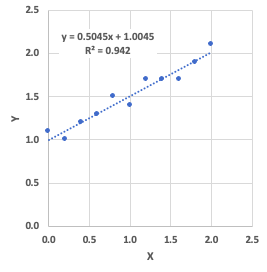
上記のようなデータに対してエクセルで近似直線を引く時、皆さんは無意識に以下のような手順を踏んでいます。

データを説明するモデルとして$y=ax+b$を仮定する。
データから最適な$a,b$をエクセルが計算する。

それでは、$a,b$をどのように計算しているか説明します。

まず、$y$と$ax+b$に分けて考えます。$y$は実際に得られている目的変数のデータで、$ax+b$は$x$のデータから$y$を予測するための関数です。

つまり、$y$と$ax+b$の間には完全なイコール関係ではなく誤差が生じています。

その二乗誤差の総和を数式で表すと、以下のようになります。

$$E(a,b)=\frac{1}{N}\sum_{i=1}^{N}{(y_i-(ax_i+b))^2}$$

$y_i,x_i$はそれぞれデータ$i$のときの$y,x$座標の値で、$N$は総サンプル数です。

この$E(a,b)$が最小になるように$a,b$の値を定めます。このパラメータの求め方を最小二乗法と言います。

$E(a,b)$をそれぞれのパラメータ$a,b$で偏微分して=0の式を連立方程式で解けば$a,b$の解が一意に定まります。

$$\partial E(a,b)/\partial a=-2\sum_{i=1}^{N}{(y_i-ax_i-b)x_i}=0$$

$$\partial E(a,b)/\partial b=-2\sum_{i=1}^{N}{(y_i-ax_i-b)x_i}=0$$

重回帰分析

重回帰分析とは複数の独立変数Xを用いて目的変数であるYを表す関数を構築することなので、重回帰分析のまず一つのゴールは目的に応じた以下の式を構築することです。

$$\boldsymbol{y}=w_0+w_1\boldsymbol{x_1}+w_2\boldsymbol{x_２}+…+w_d\boldsymbol{x_d}$$

$\boldsymbol{x_1}$, $\boldsymbol{x_2}$,…,$\boldsymbol{x_d}$は特徴量ベクトルで、学習に使用するデータセットに応じたパラメータ（ $w_0$,$w_1$,$w_2$,…,$w_d$）が定数として出力されます。

詳細は後述しますが、データ前処理に標準化を行えば$w_0=0$となり項を1つ削除する事ができます。

それでは単回帰分析の時と同様にパラメータ（ $w_0$,$w_1$,$w_2$,…,$w_d$）の求めるために重回帰分析の二乗誤差を考えましょう。

$$E(w_0,w_1,…,w_d)=\frac{1}{N}\sum_{i=1}^{N}{(y_i-(w_0+w_1x_1+w_2x_２+…+w_dx_d))^2}$$

上式は項数が多いので行列とベクトルの概念を導入します。まず説明変数のデータセット$X$は以下の行列に置き換えます。

$$X=\begin{pmatrix}
x_{1}^{0} & x_{1}^{1} & \dots & x_{1}^{d} \\
x_{2}^{0} & x_{2}^{1} & \dots & x_{2}^{d} \\
\vdots & \vdots & \ddots & \vdots \\
x_{n}^{0} & x_{n}^{1} & \dots & x_{n}^{d}
\end{pmatrix}$$

目的変数のデータセット$\boldsymbol{y}$は以下のベクトルに置き換えます。

$$\boldsymbol{y}=\begin{pmatrix}
y_{1} \\
y_{2}\\
\vdots \\
y_{n}
\end{pmatrix}$$

求めるパラメータ$\boldsymbol{w}$は以下のベクトルに置き換えます。

$$\boldsymbol{w}=\begin{pmatrix}
w_{0} \\
w_{1}\\
\vdots \\
w_{d}
\end{pmatrix}$$

行列とベクトルを用いた場合、二乗誤差は以下のように書き換える事ができます。

$$E(\boldsymbol{w})=\frac{1}{N}(\boldsymbol{y}-X\boldsymbol{w})^{T}(\boldsymbol{y}-X\boldsymbol{w})$$

行列の微分公式を用いて以下のように回帰係数を算出する事ができます。

$$\partial E(\boldsymbol{w})/\partial \boldsymbol{w}=-2X^{T}(\boldsymbol{y}-X\boldsymbol{w})=0$$

上式を解くとパラメータを求める式は以下の通りになります。

$$\boldsymbol{w}=(X^{T}X)^{-1}X^{T}\boldsymbol{y}$$

上式にそれぞれ $X,\boldsymbol{y}$ を代入するとパラメータ（ $\boldsymbol{w}$）は一意に定まります。

Pythonで重回帰分析を実装

それでは実際にPythonを使って「Wineデータセット」を用いて重回帰分析を行っていきます。

まずは使用するライブラリーをインポートします。

import numpy as np
import pandas as pd
from sklearn import datasets
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error

import numpy as np

import pandas as pd

from sklearn import datasets

import seaborn as sns

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error

次にWineデータセットを用意します。実務の状況に近づけるためにデータフレームの形でデータセットを確認します。

#========================
# データセットの準備
#========================
wine_data = datasets.load_wine()
df = pd.DataFrame(wine_data.data, columns=wine_data.feature_names)

#========================

# データセットの準備

#========================

wine_data = datasets.load_wine()

df = pd.DataFrame(wine_data.data, columns=wine_data.feature_names)

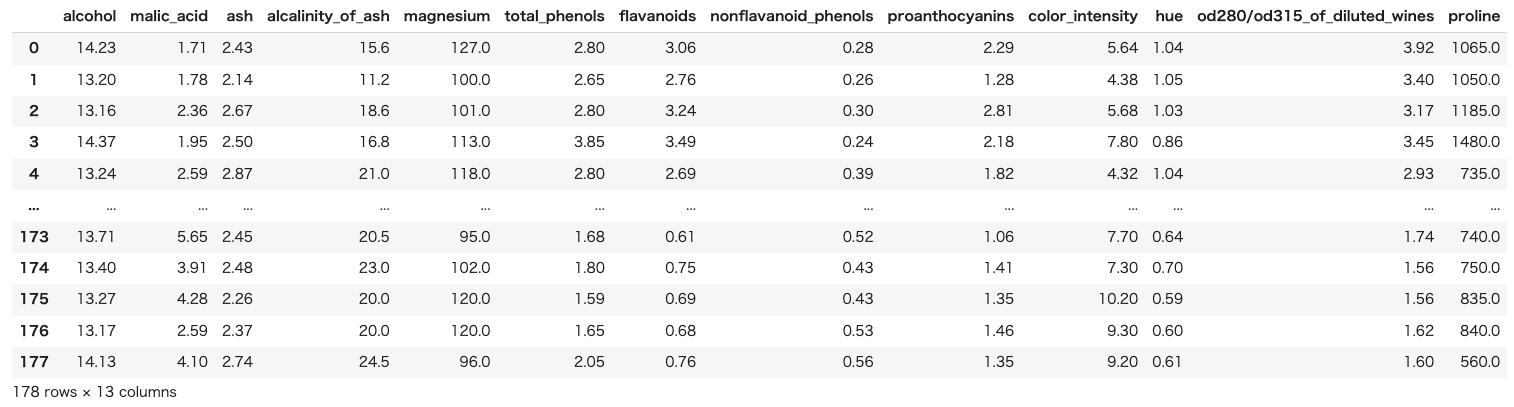
今回使うデータセットはサンプル数178、特徴量が13のデータセットです。

目的変数を”alcohol”として、他12個の特徴量から目的変数を予測する回帰モデルを構築してみます。

データセットの確認

重回帰分析の前提条件として、説明変数は独立である必要があります（理由は後述してます）。
説明変数間の独立性を一旦確認してみましょう。

#===================
# ペアプロット図の作成 #
#===================
sns.pairplot(df)

#===================
# 相関行列の作成 #
#===================
plt.rcParams["font.size"] = 10
df_corr = df.corr()
plt.figure(figsize=(8,6))
sns.heatmap(df_corr, annot=True, cmap="RdBu")

#===================

# ペアプロット図の作成 #

#===================

sns.pairplot(df)

#===================

# 相関行列の作成 #

#===================

plt.rcParams["font.size"] = 10

df_corr = df.corr()

plt.figure(figsize=(8,6))

sns.heatmap(df_corr, annot=True, cmap="RdBu")

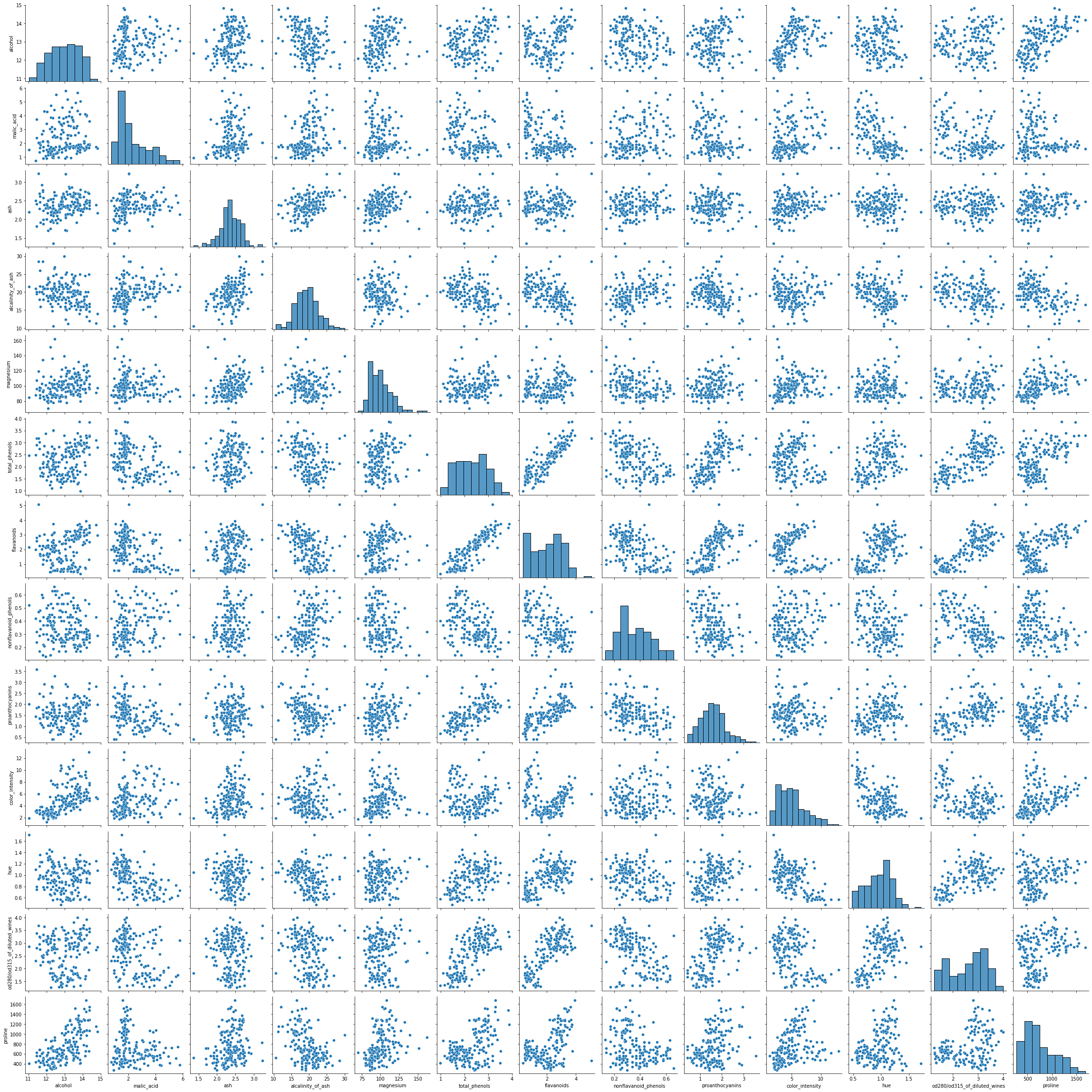
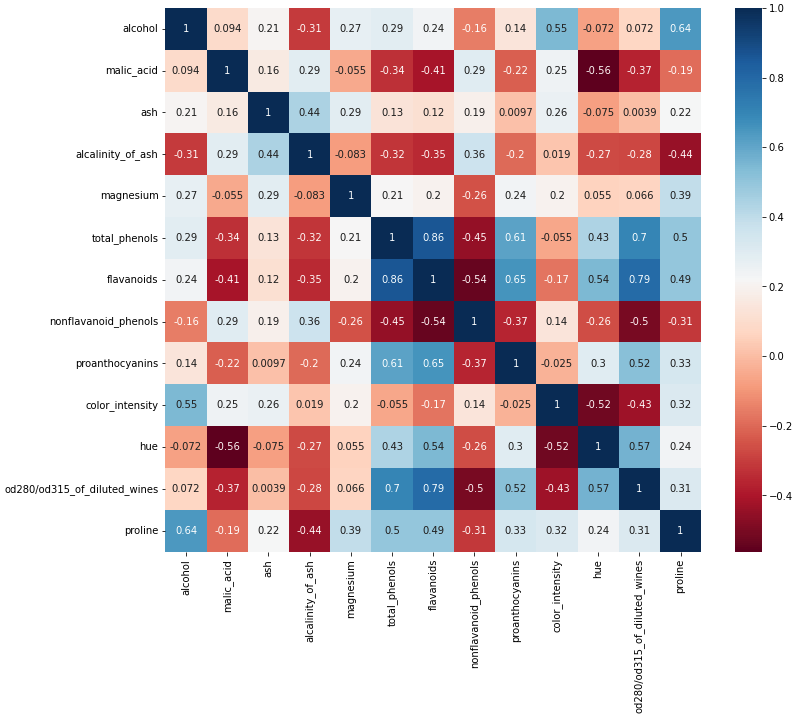
「“total_phenols” と “flavanoids”の間に相関がある」ことが気になりますね。

相関係数を確認すると”0.86″と比較的強い正の相関関係がある事がわかります。

ここで「どちらかの特徴量を消したほうが良いのかな？」と疑問に持つようになれば初学者の壁を一枚破ったことになります。

特徴量を削除すべきかどうかの閾値として相関係数の絶対値が0.95以上という論文もあるらしいのですが、ここでは一旦削除せずに分析を進めていきましょう。

構築したモデルを確認して、再度特徴量の削除を検討すればOKです。

どちらの特徴量を消すかを検討する場合は、現場の意見も参考にしましょう！

前処理

重回帰分析を行う前にデータセットの標準化を行います。

標準化とはデータの平均を0に、分散（標準偏差も）は1に変換することを言います。

標準化する事で物理次元を無次元化する事ができるので、全ての特徴量を平等に評価する事ができます。

また、目的変数も標準化するため平均値が0となり、予測する側の関数f(X)の切片となる「$w_0=0$」になります。

それではコードを確認していきましょう。

#==================================
# データを学習データとテストデータに分割する
#==================================
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100)

#========================
# データセットの標準化
#========================
autscaled_X_train = (X_train - X_train.mean())/X_train.std()
autscaled_X_test = (X_test - X_train.mean())/X_train.std()
autscaled_y_train = (y_train - y_train.mean())/y_train.std()
autscaled_y_test = (y_test - y_train.mean())/y_train.std()

#==================================

# データを学習データとテストデータに分割する

#==================================

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100)

#========================

# データセットの標準化

#========================

autscaled_X_train = (X_train - X_train.mean())/X_train.std()

autscaled_X_test = (X_test - X_train.mean())/X_train.std()

autscaled_y_train = (y_train - y_train.mean())/y_train.std()

autscaled_y_test = (y_test - y_train.mean())/y_train.std()

先頭5行のみの出力ですが、標準化すると以下のようにデータの値が変わります。

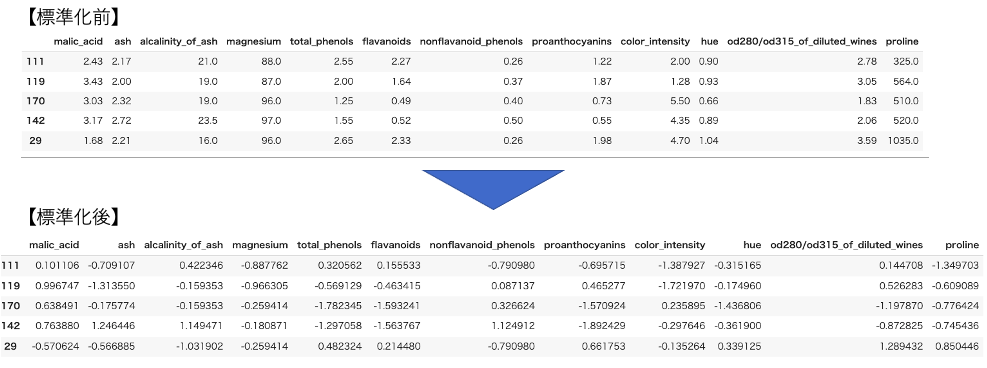
重回帰分析の実装

準備が整いましたので、早速重回帰分析を実装していきましょう！

#========================
# モデルの定義
#========================
model = LinearRegression()
model.fit(autscaled_X_train, autscaled_y_train)

#========================

# モデルの定義

#========================

model = LinearRegression()

model.fit(autscaled_X_train, autscaled_y_train)

上記コードを走らせることでパラメータ（ $\boldsymbol{w}$）が最小二乗法により計算されます。

以下コードにより、計算されたパラメータを出力することできます。

model.coef_

1	model.coef_

上記の通り、パラメータが計算された事が確認できました。

また、最小二乗法をスクラッチで実装します。scikit-learnの計算結果と同じであることを確認してみてください。

X = autscaled_X_train.values
y = autscaled_y_train.values

XX_inv = np.linalg.inv(X.T @ X) #XXの逆行列

print(XX_inv@(X.T)@y) #最小二乗法

X = autscaled_X_train.values

y = autscaled_y_train.values

XX_inv = np.linalg.inv(X.T @ X) #XXの逆行列

print(XX_inv@(X.T)@y) #最小二乗法

重回帰分析の解析結果がどの程度の予測精度を有しているかを直感的に理解するためにyyプロットを作図します。

plt.figure(figsize=(6,6))

predicte_y_train = model.predict(autscaled_X_train)*y_train.std()+y_train.mean()
predicte_y_test = model.predict(autscaled_X_test)*y_train.std()+y_train.mean()

plt.scatter(y_train, predicte_y_train,color='blue',alpha=0.5,label="Train")
plt.scatter(y_test, predicte_y_test,color='red',alpha=0.5,label="Test")
plt.plot([10.5,15],[10.5,15], 'k-',alpha=0.5)
plt.xlim(10.5,15)
plt.ylim(10.5,15)
plt.xlabel("Actual y",fontsize=14)
plt.ylabel("Estimatedl y",fontsize=14)
plt.legend(loc="best")
plt.show()

plt.figure(figsize=(6,6))

predicte_y_train = model.predict(autscaled_X_train)*y_train.std()+y_train.mean()

predicte_y_test = model.predict(autscaled_X_test)*y_train.std()+y_train.mean()

plt.scatter(y_train, predicte_y_train,color='blue',alpha=0.5,label="Train")

plt.scatter(y_test, predicte_y_test,color='red',alpha=0.5,label="Test")

plt.plot([10.5,15],[10.5,15], 'k-',alpha=0.5)

plt.xlim(10.5,15)

plt.ylim(10.5,15)

plt.xlabel("Actual y",fontsize=14)

plt.ylabel("Estimatedl y",fontsize=14)

plt.legend(loc="best")

plt.show()

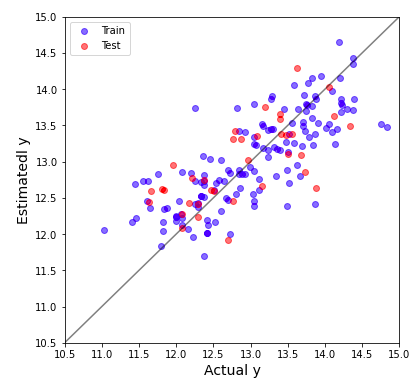
横軸には実際にデータセットにあった目的変数の実測値、縦軸には機械学習に予測させた値を示しています。縦横同じスケールで図示しているため、全てのプロットが斜めの線に近いと予測精度が高い機械学習モデルを構築できたことになります。

以下のコードから構築したモデルの評価指標を出力できます。

# トレーニングデータのr2, RMSE, MAE
print('r^2 for training data :', r2_score(y_train, predicte_y_train))
print('RMSE for training data :', mean_squared_error(y_train, predicte_y_train, squared=False))
print('MAE for training data :', mean_absolute_error(y_train, predicte_y_train))
print("==========================================================")
# テストデータのr2, RMSE, MAE
print('r^2 for test data :', r2_score(y_test, predicte_y_test))
print('RMSE for test data :', mean_squared_error(y_test, predicte_y_test, squared=False))
print('MAE for test data :', mean_absolute_error(y_test, predicte_y_test))