こんにちは、nissyです。
今回は「重回帰分析を行う上での注意点」について記事にしたいと思います。
重回帰分析については以下の記事で説明しているので、合わせて読んでみてください。

重回帰分析を行う前後での注意点について説明しますが、これは機械学習が自動で補ってくれるものではなく、人が確認して気付かなければなりません。
機械学習は、これらのポイントに注意しなくても何かしらのアウトプットを出力してくれますが、そのモデルの予測精度が低くなったり、理論(真のモデル)から大きく外れたアウトプットを出してしまうことがあります。
分析前に実施すること
説明変数の独立性
重回帰分析では、説明変数同士が独立していることが重要です。
以下のように説明変数間で強い相関を持つ場合(言い換えると、複数の説明変数が同じ情報を表している場合)、モデルのパラメーターの推定が不安定になり、信頼性の低い予測結果をもたらす可能性があります。
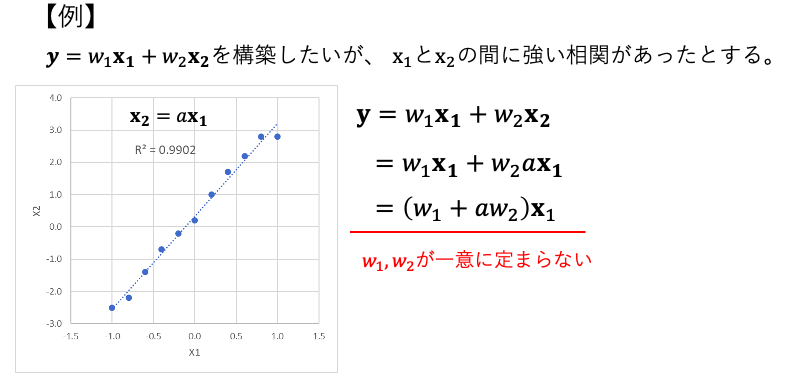
このような説明変数間に強い相関がある現象のことを「多重共線性」と言います。

それでは実際に多重共線性のあるデータセットを作成し、重回帰分析を実施しみましょう。
使用するライブラリーをインポートします。
|
1 2 3 4 5 6 7 |
import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error |
次に多重共線性のあるデータセットを作成します。今回は目的変数と説明変数の間に以下のような関係性があると仮定します。
$$\boldsymbol{y}=2\boldsymbol{x_1}+3\boldsymbol{x_2}+4\boldsymbol{x_3}+5\boldsymbol{x_4}$
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 説明変数を生成する x1, x2, x3, x4 = np.random.normal(0, 1, (4, 100)) # 説明変数間の相関係数行列を作成する corr_matrix = np.array([[1.0, 0.8, 0.5, 0.9], [0.8, 1.0, 0.3, 0.9], [0.5, 0.3, 1.0, 0.9], [0.9, 0.9, 0.9, 1.0]]) # 多変量正規分布に従うデータを生成する data = np.random.multivariate_normal([0, 0, 0, 0], corr_matrix, 100) # 目的変数を作成する y = 2*x1 + 3*x2 + 4*x3 + 5*x4 + np.random.normal(0, 1, 100) # データをデータフレームに変換する df = pd.DataFrame(data, columns=['x1', 'x2', 'x3', 'x4']) df['y'] = y |
上記コードによりdfに以下のデータセットが作成されました。
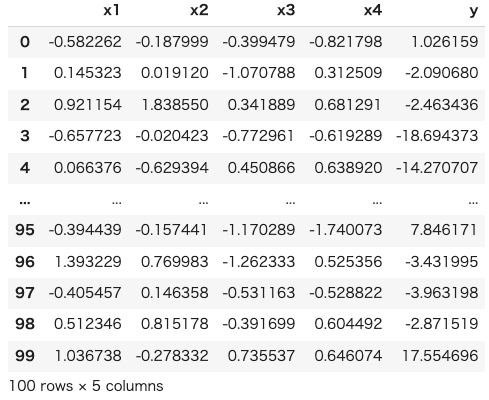
ペアプロットで散布図を確認してみます。
|
1 2 |
sns.pairplot(df.iloc[:,:-1], plot_kws={"s":20, "alpha":0.8, "linewidth":0.2, "edgecolor":"white"}) plt.show() |
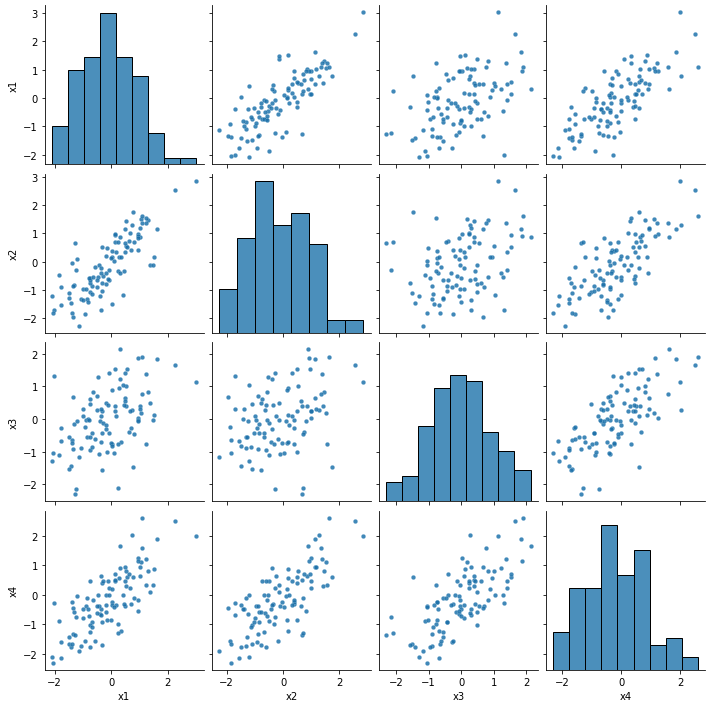
説明変数間に相関関係があるデータセットを作成する事ができました。
それでは実際に重回帰分析を行い、真のモデルと回帰係数を比較してみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
X = df.iloc[:,:-1] y = df["y"] #================================== # データを学習データとテストデータに分割する #================================== X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100) #======================== # モデルの定義 #======================== model = LinearRegression() model.fit(X_train, y_train) #======================== # 回帰係数の出力 #======================== model.coef_ |
重回帰分析より得られた回帰係数は以下の通りとなり、真のモデルとして設定した回帰係数の値と大きく異なっている事がわかります。

多重共線性を回避するためには、以下のような方法があります。
- 相関の高い説明変数を削除する
- 主成分分析などの手法を用いて新たな変数を作成する
- リッジ回帰やLASSO回帰などの正則化手法を用いる
相関の高い説明変数を削除する
以下のような相関行列を出力し相関の高い説明変数のどちらかを削除します。
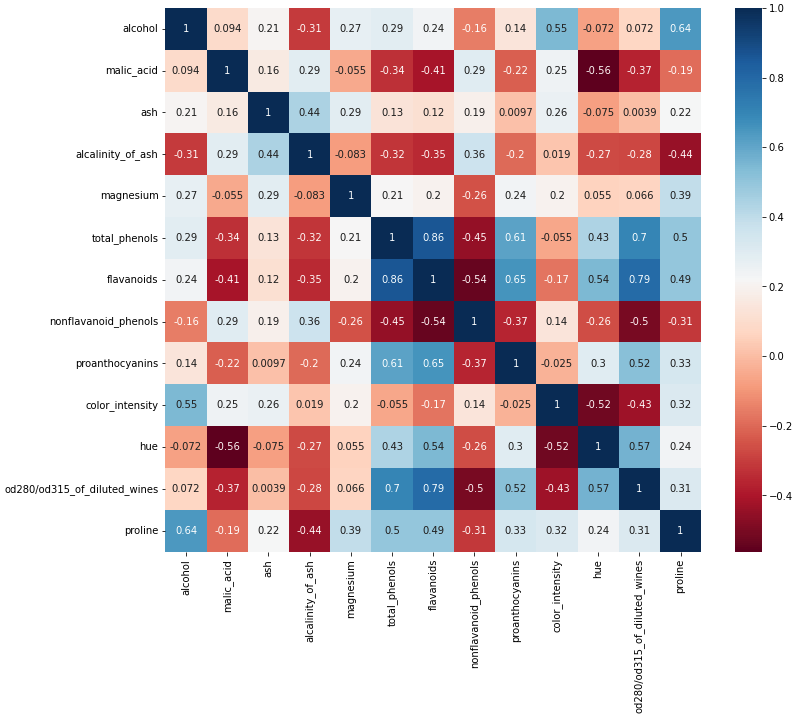
相関行列を見る上での注意点として、相関係数は特徴量間の直線的な関係(比例関係)の強さを、+1 〜−1 の間の数で表す指標です。もし特徴量間に明確な非線形の関係があった場合、相関係数は低くでます。
しかしながら、重回帰分析は説明変数と目的変数の線形関係を仮定しているため、非線形な関係がある場合には、適切なモデルが得られない可能性があります。
相関行列だけでなくペアプロットなどで散布図を確認するようにしましょう。
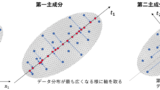
主成分分析などの手法を用いて、説明変数を線形結合した新たな変数を作成する
以下の記事で説明した通り、主成分分析を行うと特徴量間の相関関係がなくなります。
リッジ回帰やLASSO回帰などの正則化手法を用いる

こちらの手法に関する記事は現在制作中です。
データセットの標準化
データセットの標準化とは、データセットの各変数を平均が0、標準偏差が1となるように変換する処理のことです。
標準化を行うことで、以下のようなメリットがあります。
データのスケール差異の影響を排除できる
異なるスケールで表された変数を用いた分析では、値の大きさが結果に影響を与える可能性があります。標準化によって、スケール差異を排除することができ、各変数が同じ尺度で扱われるため、分析結果がより適切になります。
変数の重要度の比較が容易になる
標準化によって、各変数が同じ尺度で扱われるため、異なる変数間で重要度を比較することが容易になります。たとえば、ある変数が平均値から大きく外れる場合、その変数が結果に与える影響が大きいと考えられます。
外れ値の影響を軽減できる
外れ値は、平均値や標準偏差を大きく変化させるため、データの標準化に影響を与えます。しかし、外れ値が含まれる変数を標準化することで、外れ値の影響を軽減することができます。
分布が正規分布に近づく
標準化によって、分布が正規分布に近づくことがあります。これによって、統計的手法を適用する際に必要となる仮定(例えば、正規分布の仮定)を満たすことができるため、結果の信頼性を向上させることができます。
回帰係数が非常に大きい場合、モデルが過剰適合し未知のデータに対する予測精度が低下する可能性があります。
また、回帰係数が異なる変数間でオーダーが大きく異なる場合、回帰係数を単純に比較することはできず、スケールを統一する必要があります。
このため、データを前処理して回帰係数を1桁のオーダーに調整することで、モデルの性能が向上する可能性があります。
scikit-learnを使用して回帰分析を行う場合、回帰係数が1桁のオーダーになるようにデータを前処理することが望ましいです。
分析後に確認すること
残差の等分散性
重回帰分析では、誤差項の分散が一定であることが前提条件となります。
例えば、目的変数が予測値の大きさによって分散が増加する場合などが挙げられます。
分散が異なる場合は、正確な予測を行うことができません。
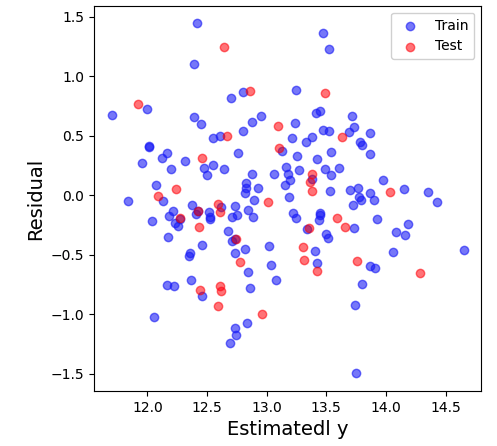
等分散性を検証するためには、残差プロットを作成します。
残差プロットから、誤差項が一定の範囲内にばらついているかを確認します。
以下に重回帰分析の記事で紹介したデータの残差プロットを示します。
https://nissyblog-2904.com/1-10/
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 残差プロット zansa_train = y_train - predicte_y_train zansa_test = y_test - predicte_y_test plt.figure(figsize=(5,5)) plt.scatter(predicte_y_train, zansa_train, color='blue',alpha=0.5,label="Train") plt.scatter(predicte_y_test, zansa_test,color='red',alpha=0.5,label="Test") plt.xlabel("Estimatedl y",fontsize=14) plt.ylabel("Residual",fontsize=14) plt.legend(loc="best") plt.show() |
残差の正規性
重回帰分析では、誤差項が正規分布に従うことが前提条件となります。
正規分布に従わない場合、偏った予測結果が導かれる可能性があります。
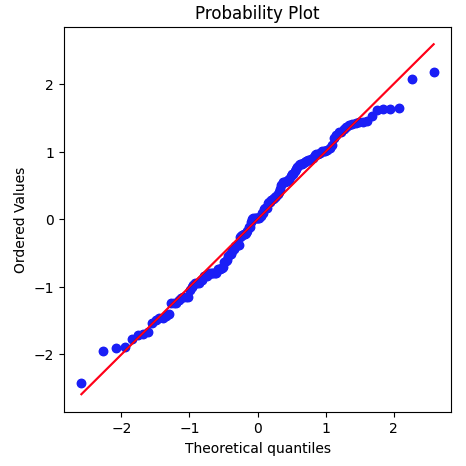
正規性を検証するためには、ヒストグラムやQQプロットを作成することができます。
ヒストグラムやQQプロットから、残差が正規分布に従っているかを確認することができます。
|
1 2 3 4 5 |
# Q-Qプロットの描画 from scipy import stats plt.figure(figsize=(5,5)) stats.probplot(y, dist="norm", plot=plt) plt.show() |
まとめ
重回帰分析を行う上で、独立性、等分散性、正規性といった前提条件を満たすことが重要です。それぞれの確認方法は以下の通りです。
- 独立性を検証するためには、相関行列を用いる
- 等分散性を検証するためには、残差プロットを用いる
- 正規性を検証するためには、ヒストグラムやQQプロットを用いる
これらの条件を満たすことで、より正確な予測を行うことができますが、実際のデータは必ずしもこれらの条件を満たしているわけではないため注意が必要です。
またデータセットを標準化することで、説明変数のスケールの違いによる影響を排除することができます。
必要に応じて適切な前処理を行い、分析後の確認も必ず行うようにしましょう。



コメント