こんにちは、nissyです。
本日は、機械学習初学者にとって重要な次のステップとなる「LASSO(Least Absolute Shrinkage and Selection Operator)」について解説していきたいと思います。
LASSOは、重回帰分析の発展形であり、正則化と特徴選択を組み合わせた強力な手法です。これにより、よりスパースで解釈しやすいモデルを構築することができます。
今回の記事では、データサイエンス初学者の皆さんが、LASSOの基本的な理解を深めることができることを目指しています。
今回は重回帰分析の知識を有している方を対象に記事を作成しています。
重回帰分析についての理解が不安な方は以下のブログを先に読んでいただくことを推奨します。

正則化の概念
機械学習やデータ解析の分野では、過学習(overfitting)や未学習(underfitting)といった問題がよく発生します。
これらの問題は、モデルがデータに対して適切なバイアスとバリアンスのバランスを見つけることが難しいためです。
正則化(regularization)は、これらの問題に対処するための一般的な手法であり、LASSO回帰はその中でも非常によく使われる手法の一つです。

実際に私も最初はLASSO回帰でモデル構築を試す事が多く、仕事でも非常に使用頻度の高いモデルです。
正則化は、過学習を防ぐための手法で、モデルの表現力に制約を加えることで実現します。具体的には、損失関数にペナルティ項を加えて、モデルのパラメータが大きくなりすぎないようにします。
正則化を用いることで、モデルのバイアスとバリアンスのバランスを適切に調整できます。バイアスはモデルが学習データに適合できるかを示し、バリアンスは新しいデータに対してモデルが適応できるかを示します。
過学習を防ぐためには、バイアスとバリアンスの適切なバランスが必要で、これは正則化パラメータを調整することで制御できます。適切な正則化パラメータを選ぶことで、モデルの予測性能を向上させることができます。
LASSOの説明
LASSOは、統計学と機械学習における重要な手法で、特徴選択と正則化を同時に行うことができます。LASSOの基本的な考え方は、モデルの表現力を制御しつつ、予測性能を最適化することです。これは、線形回帰の誤差関数にL1正則化項を追加することで実現されます。
線形回帰の誤差関数は平均二乗誤差(MSE)を最小化することを目指しますが、LASSOではこの誤差関数にパラメータの絶対値の和(L1ノルム)に比例するペナルティ項(L1正則化項)を加えます。つまり、LASSOの誤差関数は以下のようになります。
$$E(\theta)=\frac{1}{N}\sum_{i=1}^{N}{(h_{\theta}(x^{(i)}) – y^{(i)})^2} + \alpha \sum_{j=1}^{D} |\theta_j|$$
ここで、\(h_{\theta}(x^{(i)})\)はモデルの予測値、\(y_i\)は実際の値、\(\alpha\)はモデルのハイパーパラメータ、\(N\)はデータの数、\(D\)は特徴量の数、\(\lambda\)は正則化パラメータを表します。
このペナルティ項は、モデルのパラメータが大きくなることを抑制し、モデルの表現力を制限します。これにより、過学習を防ぎつつ、モデルの予測性能を維持することが可能となります。
LASSOのもう一つの重要な特性は特徴選択です。LASSOは不要な特徴量のパラメータ(回帰係数)をゼロにすることができます。これはL1正則化がスパースな解を生む性質によるもので、この特性によりモデルが自動的に重要な特徴量だけを選択することが可能となります。これは、特に特徴の数が多く、どの特徴量が重要であるかを事前に判断するのが難しい場合に有用です。
このようにLASSOはモデルの表現力を制御し、過学習を防ぐだけでなく、重要な特徴量を自動的に選択することで、モデルの解釈性を向上させることができます。
PythonでLASSOの回帰を実装
それでは実際にPythonを使って「ボストン住宅価格データセット」を用いてLASSO回帰分析を行っていきます。
まずは使用するライブラリーをインポートします。
|
1 2 3 4 5 6 7 8 9 10 |
import pandas as pd import seaborn as sns from sklearn.datasets import load_boston import numpy as np import matplotlib.pyplot as plt import japanize_matplotlib from sklearn.model_selection import train_test_split from sklearn.linear_model import LassoCV from sklearn.linear_model import LassoLarsIC from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error |
次にボストン住宅価格データセットを用意します。実務の状況に近づけるためにデータフレームの形でデータセットを確認します。
|
1 2 3 4 5 6 |
#======================== # データセットの準備 #======================== boston = load_boston() df = pd.DataFrame(boston.data, columns=boston.feature_names) df['PRICE'] = boston.target |
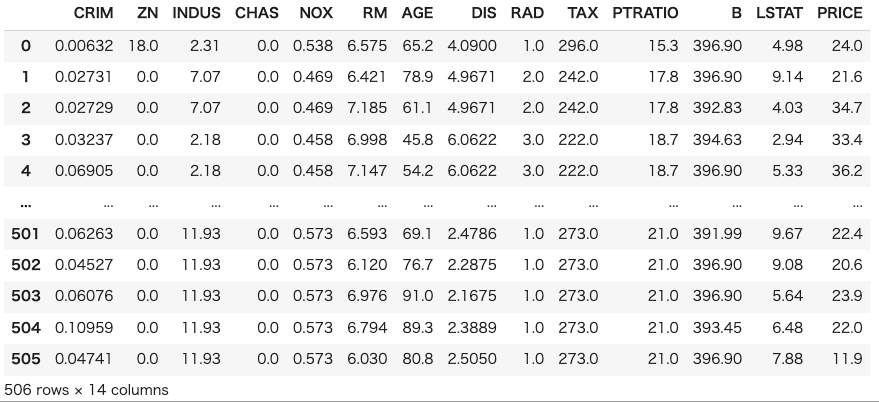
今回使うデータセットはサンプル数506、特徴量が13のデータセットです。
目的変数を”PRICE”として、他12個の特徴量から目的変数を予測する回帰モデルを構築してみます。
以下のコードでデータを学習データとテストデータに分割し、それぞれを標準化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#================================== # データを学習データとテストデータに分割する #================================== X = pd.DataFrame(boston.data, columns=boston.feature_names) y = boston.target X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100) #======================== # データセットの標準化 #======================== autscaled_X_train = (X_train - X_train.mean())/X_train.std() autscaled_X_test = (X_test - X_train.mean())/X_train.std() autscaled_y_train = (y_train - y_train.mean())/y_train.std() autscaled_y_test = (y_test - y_train.mean())/y_train.std() |
今回はハイパーパラメータである\(\alpha\)を3通りの方法で決めてみようと思います。それぞれ、
- 交差検証誤差
- AIC(赤池情報量基準)
- BIC(ベイズ情報量基準)
詳細は改めて別の記事でご紹介しようと思います。以下のコードでモデルの定義および学習を実行します。
|
1 2 3 4 5 6 7 8 9 10 |
#================================== # モデルの定義 #================================== model_lasso_cv = LassoCV(cv=17, alphas=np.logspace(-7,2,1000),max_iter=10000) model_lasso_aic = LassoLarsIC(criterion='aic') model_lasso_bic = LassoLarsIC(criterion='bic') model_lasso_cv.fit(autscaled_X_train, autscaled_y_train) model_lasso_aic.fit(autscaled_X_train, autscaled_y_train) model_lasso_bic.fit(autscaled_X_train, autscaled_y_train) |
LASSO回帰の解析結果がどの程度の予測精度を有しているかを直感的に理解するためにyyプロットを作図します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
plt.figure(figsize=(5,5)) predicte_y_train = model_lasso_cv.predict(autscaled_X_train)*y_train.std()+y_train.mean() predicte_y_test = model_lasso_cv.predict(autscaled_X_test)*y_train.std()+y_train.mean() plt.scatter(y_train, predicte_y_train,color='blue',alpha=0.5,label="Train") plt.scatter(y_test, predicte_y_test,color='red',alpha=0.5,label="Test") plt.plot([-5.,60],[-5,60], 'k--',alpha=0.5) plt.xlim(-5,55) plt.ylim(-5,55) plt.xlabel("Actual y",fontsize=14) plt.ylabel("Estimatedl y",fontsize=14) plt.legend(loc="best") plt.show() # トレーニングデータのr2, RMSE, MAE print('r^2 for training data :', r2_score(y_train, predicte_y_train)) print('RMSE for training data :', mean_squared_error(y_train, predicte_y_train, squared=False)) print('MAE for training data :', mean_absolute_error(y_train, predicte_y_train)) print("==========================================================") # テストデータのr2, RMSE, MAE print('r^2 for test data :', r2_score(y_test, predicte_y_test)) print('RMSE for test data :', mean_squared_error(y_test, predicte_y_test, squared=False)) print('MAE for test data :', mean_absolute_error(y_test, predicte_y_test)) |
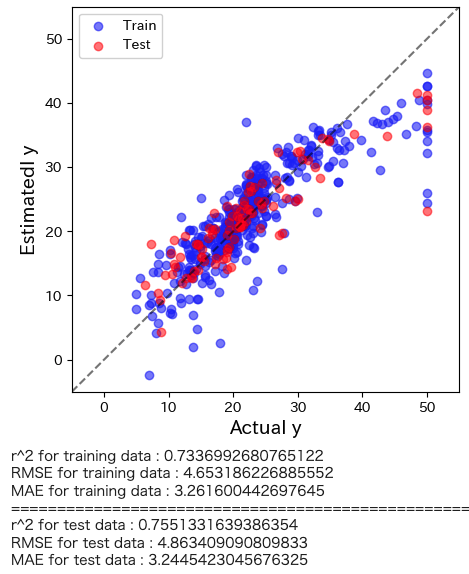
計算によって得られた回帰係数をグラフ化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# LASSO回帰の係数を取得 lasso_coefs = model_lasso_cv.coef_ # カラム名を取得 column_names = X.columns # グラフのスタイルを設定 sns.set(style='whitegrid') # プロットのサイズを調整 plt.figure(figsize=(12, 6)) # 係数のバー表示 plt.bar(column_names, lasso_coefs) # 軸のラベルを設定 plt.xlabel('Feature Names') plt.ylabel('Coefficient Value') # x軸のラベルを回転させて表示 # plt.xticks(rotation=90) # グリッド線を表示 plt.grid(True) # タイトルを設定 plt.title('LASSO Coefficients') # グラフを表示 plt.show() |
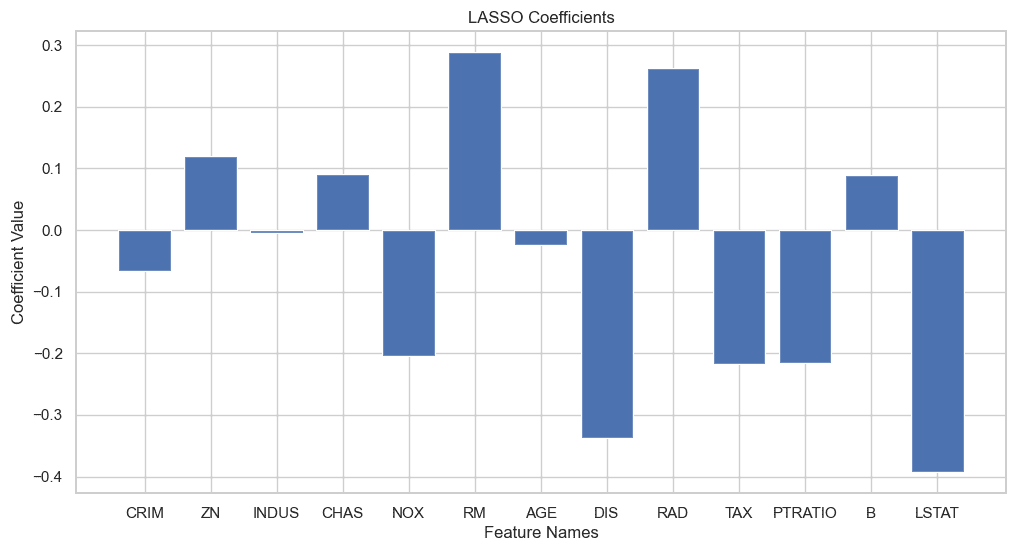
学習曲線(交差検証誤差)
ハイパーパラメータチューニングの学習曲線を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 交差検証誤差 (CVE) の算出と alpha の取得 CVEs = np.mean(model_lasso_cv.mse_path_, axis=1) alphas = model_lasso_cv.alphas_ # 交差検証誤差のプロット plt.figure() plt.plot(alphas, CVEs, label='CVE', linestyle='-', linewidth=2, marker='.',color="blue") plt.xscale("log") plt.yscale("log") # 最適化された alpha のプロット CVE_min = np.min(CVEs) CVE_max = np.max(CVEs) plt.axvline(model_lasso_cv.alpha_, 0, 100, linestyle='--', color="red", label=f'Optimal alpha = {model_lasso_cv.alpha_:.3f}', linewidth=1) # グラフの範囲設定 plt.ylim(0.9 * CVE_min, 1.1 * CVE_max) # グラフのタイトルとラベル plt.title("Cross-Validation Error (CVE) vs. LASSO Parameter (alpha)") plt.xlabel("Log-scaled LASSO Parameter (alpha)") plt.ylabel("CVE") plt.legend() # グラフ表示 plt.show() |

学習曲線(AIC、BIC)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# AIC と BIC に基づく alpha の推移をプロット plt.figure() plt.plot(model_lasso_aic.alphas_, model_lasso_aic.criterion_, label='AIC', linestyle='--', linewidth=2, marker='o') plt.plot(model_lasso_bic.alphas_, model_lasso_bic.criterion_, label='BIC', linestyle='-.', linewidth=2, marker='s') plt.xscale("log") plt.yscale("log") # AIC と BIC の最小値がどこにあるかを示す縦棒を引く min_aic_index = np.argmin(model_lasso_aic.criterion_) min_bic_index = np.argmin(model_lasso_bic.criterion_) plt.axvline(np.log10(model_lasso_aic.alphas_[min_aic_index]), color='blue', label=f'AIC optimal alpha = {model_lasso_aic.alphas_[min_aic_index]:.3f}', linestyle='--', linewidth=2) plt.axvline(np.log10(model_lasso_bic.alphas_[min_bic_index]), color='red', label=f'BIC optimal alpha = {model_lasso_bic.alphas_[min_bic_index]:.3f}', linestyle='-.', linewidth=2) # グラフのタイトルとラベル plt.title("AIC and BIC vs. Log-scaled LASSO Parameter (alpha)") plt.xlabel("Log-scaled LASSO Parameter (alpha)") plt.ylabel("AIC / BIC") plt.legend() # グラフ表示 plt.show() |
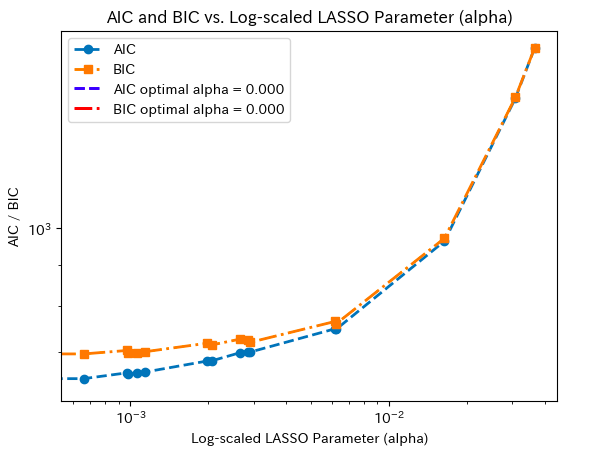
今回のデータセットではAIC、BICで正則化パラメータを決めると0となり、スパース性は有していない事がわかります。
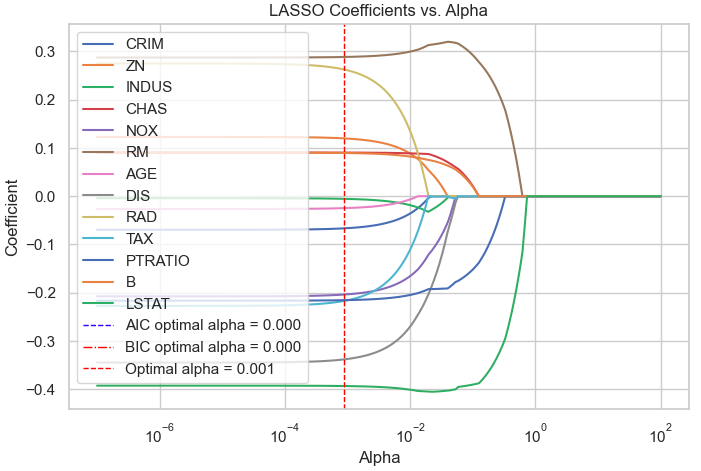
係数プロット
それでは正則化パラメータ\(\alpha\)を変えた時の各特徴量の回帰係数がどのように変化するかを確認してみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
from sklearn.linear_model import Lasso coef = pd.DataFrame() for i in range(len(alphas)): lasso = Lasso(alpha=alphas[i]) lasso.fit(autscaled_X_train, autscaled_y_train) coef = coef.append(pd.DataFrame(lasso.coef_).T) # グラフの描画 plt.figure(figsize=(8,5)) for feature in feature_names: plt.plot(coef['alphas'], coef[feature], label=feature) # グラフのタイトルとラベル plt.title("LASSO Coefficients vs. Alpha") plt.xlabel("Alpha") plt.ylabel("Coefficient") plt.xscale("log") plt.axvline(np.log10(model_lasso_aic.alphas_[min_aic_index]), color='blue', label=f'AIC optimal alpha = {model_lasso_aic.alphas_[min_aic_index]:.3f}', linestyle='--', linewidth=1) plt.axvline(np.log10(model_lasso_bic.alphas_[min_bic_index]), color='red', label=f'BIC optimal alpha = {model_lasso_bic.alphas_[min_bic_index]:.3f}', linestyle='-.', linewidth=1) plt.axvline(model_lasso_cv.alpha_, 0, 100, linestyle='--', color="red", label=f'Optimal alpha = {model_lasso_cv.alpha_:.3f}', linewidth=1) # 凡例 plt.legend(loc="best") # グラフ表示 plt.show() |
まとめ
今日はLASSOという重要な機械学習の手法について学びました。LASSOは、特徴選択と正則化を同時に行うことで、モデルの複雑さを制御し、予測性能を最適化することが可能です。そして、その実装はPythonを使って比較的簡単に行うことができます。
これからも機械学習の学習を進めていく中で、LASSOは必ずと言っていいほど出てくる重要な手法です。ぜひこの機会にPythonでの実装に挑戦してみてください。この記事があなたの学習の一助となれば幸いです。



コメント