こんにちは、nissyです。
マテリアルズ・インフォマティクスの業界で有名な明治大学の金子弘昌先生のブログにこのような記事が掲載されていました。
私は金子先生が執筆された著書を活用して勉強してきましたが、今の今までガウス過程回帰のカーネル関数の違いについて深く考えてきませんでした。
この機会にカーネル関数の違いによるモデルの振る舞いについてどのような違いがあるのか
興味を持ったので、私なりに検証してみたいと思います。
|
|
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/2eaa35ab.09768959.2eaa35ac.789bf136/?me_id=1213310&item_id=20351134&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F5300%2F9784065235300.jpg%3F_ex%3D240x240&s=240x240&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
金子先生の記事の要点
まず金子先生のブログの要点についてまとめます。
- 外挿領域の探索方法としてベイズ最適化が存在し、これはガウス過程回帰を用いる
- ガウス過程回帰でモデル構築時、カーネル関数の選択が重要。
- ガウシアンカーネル（RBFカーネル）等の距離に基づくカーネル関数では、x の外挿が進むと予測値の方向が不明確になる可能性がある。
- x の外挿領域の方向性を明確にするために、カーネル関数に線形項を追加する手法がある
実際に書籍で紹介しているガウス過程回帰のカーネル関数は以下の通りです。
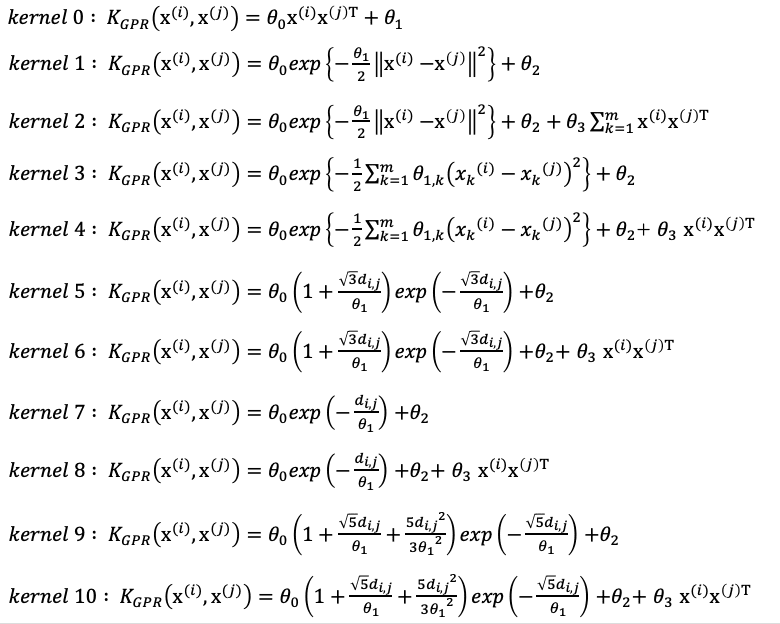
数式だけ見ても何がなんだが全然わからないnissy……
金子先生の作成したコードには、この10種類のカーネル関数の中からCV誤差が最小になるモデルが選択されるようにコードが書かれています。
それでは実際にpython環境でカーネル関数の違いについて確認していきましょう。
カーネル関数の違いを実装する
まずは予測させるモデルを設定し、そこから15サンプルほどデータを生成させます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as np import matplotlib.pyplot as plt # データ生成関数の定義 def true_function(x): return np.sin(x)*3+2*x # トレーニングデータの生成 np.random.seed(100) X_train = np.sort(np.random.uniform(0, 10, 15))[:, np.newaxis] y_train = true_function(X_train).ravel() + np.random.normal(0, 1.5, X_train.shape[0]) # テストデータの生成 X_test = np.linspace(0, 10, 1000)[:, np.newaxis] y_test = true_function(X_test).ravel() # データのプロット plt.figure(figsize=(10, 6)) plt.scatter(X_train, y_train, c='r', s=50, zorder=10, edgecolors=(0, 0, 0)) plt.plot(X_test, y_test, c='k', lw=2, zorder=9) plt.title("Data and true function") plt.tight_layout() plt.show() |
以下のようなデータが得られました。黒い線が求めるべき真のモデルで、プロットが真のモデルから生成されたサンプルになります。
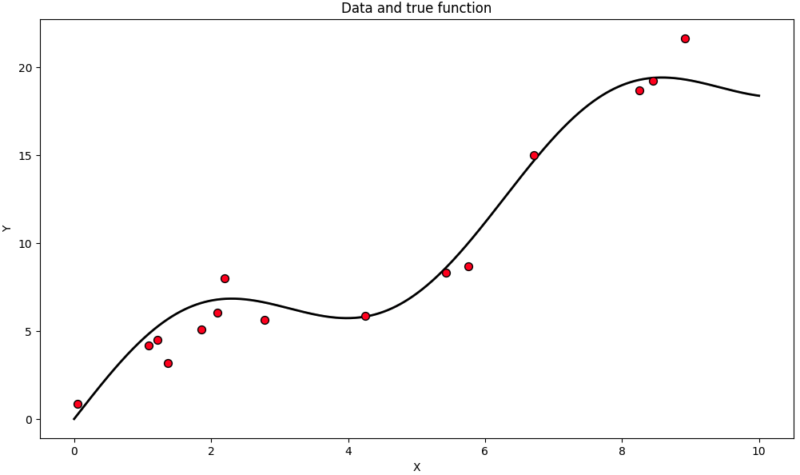
この生成したサンプルデータに対して、カーネル関数の異なるガウス過程回帰でフィッティングを行ってみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF, ConstantKernel as C, DotProduct, ExpSineSquared # カーネル関数の定義 # カーネル 11 種類 kernels = [ConstantKernel() * DotProduct() + WhiteKernel(), ConstantKernel() * RBF() + WhiteKernel(), ConstantKernel() * RBF() + WhiteKernel() + ConstantKernel() * DotProduct(), ConstantKernel() * RBF(np.ones(X_train.shape[1])) + WhiteKernel(), ConstantKernel() * RBF(np.ones(X_train.shape[1])) + WhiteKernel() + ConstantKernel() * DotProduct(), ConstantKernel() * Matern(nu=1.5) + WhiteKernel(), ConstantKernel() * Matern(nu=1.5) + WhiteKernel() + ConstantKernel() * DotProduct(), ConstantKernel() * Matern(nu=0.5) + WhiteKernel(), ConstantKernel() * Matern(nu=0.5) + WhiteKernel() + ConstantKernel() * DotProduct(), ConstantKernel() * Matern(nu=2.5) + WhiteKernel(), ConstantKernel() * Matern(nu=2.5) + WhiteKernel() + ConstantKernel() * DotProduct()] # カーネル関数の名前 # kernel_names = ["RBF", "Linear", "Periodic"] plt.figure(figsize=(14, 10)) for i, kernel in enumerate(kernels): # ガウス過程回帰のモデルの初期化と学習 gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10, alpha=0.1) gp.fit(X_train, y_train) # 予測 y_pred, sigma = gp.predict(X_test, return_std=True) # プロット plt.subplot(3, 4, i+1) plt.scatter(X_train, y_train, c='r', s=50, zorder=10, edgecolors=(0, 0, 0)) plt.plot(X_test, y_test, 'k', lw=1, zorder=9) plt.plot(X_test, y_pred, 'b', lw=2, zorder=10) plt.fill_between(X_test.ravel(), y_pred - 1.96*sigma, y_pred + 1.96*sigma, alpha=0.2, color='k') plt.title(f"Kernel: {i}") plt.tight_layout() plt.show() |
フィッティングした結果が以下の通りです。
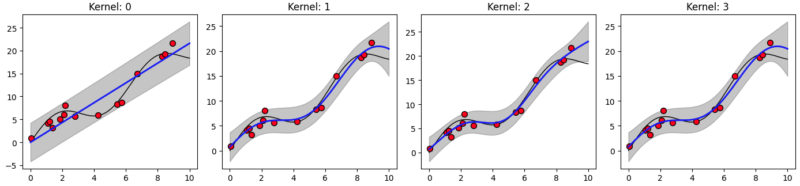
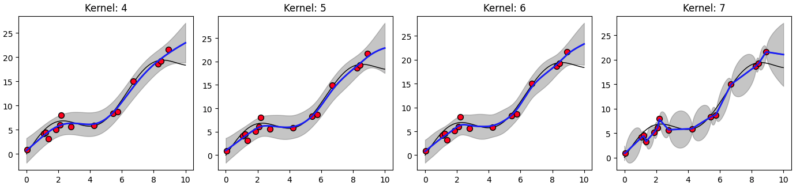
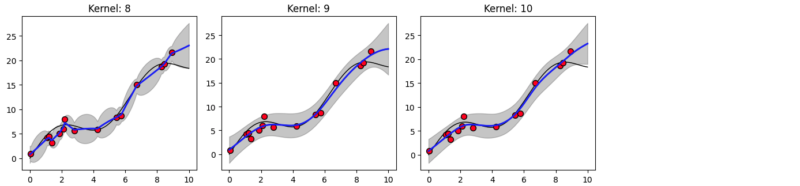
各グラフの横軸10付近に着目してください。この中でカーネル関数に線形項が入っているのが偶数番のkernel 2, 4, 6, 8, 10 です。それらはXの値が大きいサンプルの傾向を反映して、外挿を予測していることがわかります。
このことが金子先生のブログにも書かれている「外挿の方向が定めやすい」ということがわかりました。
しかしながら、それが実験値と必ずしも合致するわけではないということ、それにより線形項を含むカーネル関数を選択した際、予測性能が下がる場合も考慮する必要があるということは肝に命じておきましょう。
まとめ
今回は金子先生のブログ記事をもとに、ガウス過程回帰のカーネル関数の違いについて深掘りしてみました。カーネル関数に線形項を入れることで、外挿に近いサンプルに追従した形でモデルを予測することが可視化できました。これを金子先生は「外挿の方向が定めやすい」というように表現しているのだと思います。
しかしながら、線形項を含むカーネル関数を選択した際、予測性能が下がる場合も考慮する必要があるということに注意をしながら、モデル構築する前にしっかりと仮説を立ててモデル選択をしなければならないと考えさせられました。
コメント