こんにちはnissyです。
最近データ分析で化学構造を取り扱うテーマに携わらせていただきました。
私としては初めての経験で、日々勉強、勉強でした!
今回は、化学構造のSMILESをフィンガープリントに変換し、それらを次元削減することによりデータセットのケミカルスペースを可視化したいと思います。
次元削減にはt-SNEとUMAPという2つのアルゴリズムを利用します。
どちらも非線形の次元削減アルゴリズムとなりますが、
得られるアウトプットとしてどのような違いが生じるか観察していきましょう!!
データセットの準備 SMILESのフィンガープリント変換
まずは、データセットを読み込んで次元削減する手前の前処理を実施していきます!
データセットは明治大学金子研究室で公開しているデータセットを利用しました
1290分子の水溶解度(LogS)データ
ライブラリーを読み込みます
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import matplotlib.pyplot as plt import numpy as np import pandas as pd from scipy.spatial import distance from sklearn.manifold import TSNE import umap import mpl_toolkits.mplot3d import os import glob from tqdm.notebook import tqdm import time from rdkit import Chem from rdkit.Chem import AllChem, Draw from rdkit.Chem.Draw import rdMolDraw2D from time import time from tqdm.notebook import tqdm from time import time from tqdm import tqdm import seaborn as sns |
データセットを読み込んで、中身を確認します。
|
1 2 3 |
df = pd.read_csv('SMILES_logS_データセット.csv') print("データセットのサンプル数:",len(df)) df.head() |
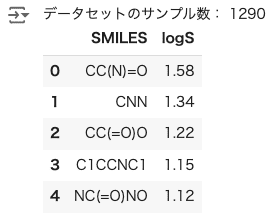
SMILESをフィンガープリントに変換します!
|
1 2 3 4 5 6 7 8 9 10 |
#================================ # SMILES⇒ECFP4への変換 #================================ radius= 2 bit =8192 mols_list = [Chem.MolFromSmiles(smiles) for smiles in df["SMILES"]] ECFP = [AllChem.GetMorganFingerprintAsBitVect(mol, radius,bit) for mol in mols_list] df_X = pd.DataFrame(np.array(ECFP, int)) df_X |
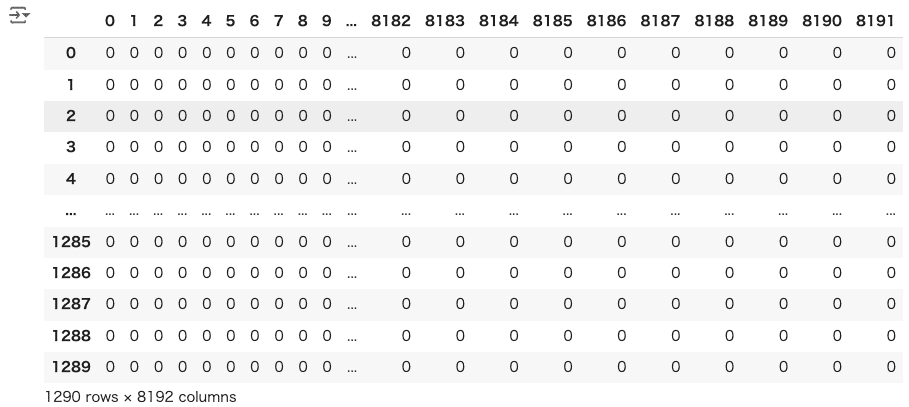
以上で準備完了です!!
t-SNEによる可視化
それでは、フィンガープリントを次元削減していきます。
まずはt-SNEの実装コードを紹介します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
#========================== # K3nerror #========================== def k3nerror(X1, X2, k): """ k-nearest neighbor normalized error (k3n-error) When X1 is data of X-variables and X2 is data of Z-variables (low-dimensional data), this is k3n error in visualization (k3n-Z-error). When X1 is Z-variables (low-dimensional data) and X2 is data of data of X-variables, this is k3n error in reconstruction (k3n-X-error). k3n-error = k3n-Z-error + k3n-X-error Parameters ---------- X1: numpy.array or pandas.DataFrame X2: numpy.array or pandas.DataFrame k: int The numbers of neighbor Returns ------- k3nerror : float k3n-Z-error or k3n-X-error """ X1 = np.array(X1) X2 = np.array(X2) X1_dist = distance.cdist(X1, X1) X1_sorted_indices = np.argsort(X1_dist, axis=1) X2_dist = distance.cdist(X2, X2) for i in range(X2.shape[0]): _replace_zero_with_the_smallest_positive_values(X2_dist[i, :]) I = np.eye(len(X1_dist), dtype=bool) neighbor_dist_in_X1 = np.sort(X2_dist[:, X1_sorted_indices[:, 1:k+1]][I]) neighbor_dist_in_X2 = np.sort(X2_dist)[:, 1:k+1] sum_k3nerror = ( (neighbor_dist_in_X1 - neighbor_dist_in_X2) / neighbor_dist_in_X2 ).sum() return sum_k3nerror / X1.shape[0] / k def _replace_zero_with_the_smallest_positive_values(arr): """ Replace zeros in array with the smallest positive values. Parameters ---------- arr: numpy.array """ arr[arr==0] = np.min(arr[arr!=0]) |
t-SNEのハイパーパラメータであるperplexityを最適化します。
探索範囲は「0〜サンプル数」の間を探索します。
|
1 2 3 4 5 6 7 8 |
#================================== # 初期値パラメータ #================================== k_in_k3nerror = 10 random_state_number = 100 #検討するperplexityの条件 検討範囲0~サンプル数 candidates_of_perplexity = np.arange(5, 1290, 100, dtype=int) #np.arange(始点, 終点, 刻み幅, dtype=int) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# perplexityの最適化 k3nerrors = list() # 計測開始 start_time = time() # tqdmを使用して進捗バーを表示 for perplexity in tqdm(candidates_of_perplexity): Z_in_perplexity_optimization = TSNE(perplexity=perplexity, n_components=2, init='pca', random_state=random_state_number).fit_transform(df_X) scaled_Z_in_perplexity_optimization = (Z_in_perplexity_optimization - Z_in_perplexity_optimization.mean( axis=0)) / Z_in_perplexity_optimization.std(axis=0, ddof=1) k3nerrors.append( k3nerror(df_X, scaled_Z_in_perplexity_optimization, k_in_k3nerror) + k3nerror( scaled_Z_in_perplexity_optimization, df_X, k_in_k3nerror)) # 計測終了 end_time = time() # 完了までの時間を表示 print(f"Total time: {end_time - start_time} seconds") |
結果を確認してみましょう!
|
1 2 3 4 5 6 |
plt.plot(candidates_of_perplexity, k3nerrors, "b.") plt.xlabel("perplexity") plt.ylabel("k3n-errors") plt.show() optimal_perplexity = candidates_of_perplexity[np.where(k3nerrors == np.min(k3nerrors))[0][0]] print(optimal_perplexity) |
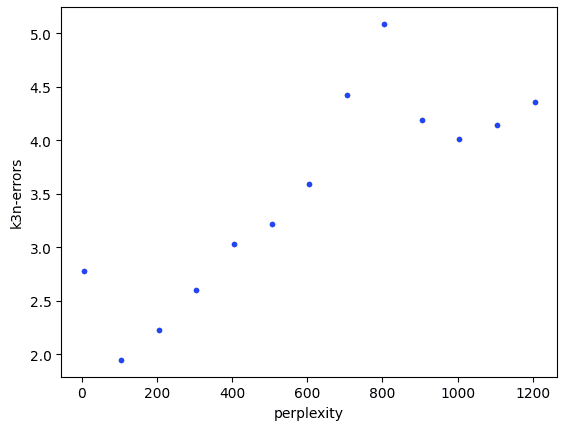
k3n-errorsの値が最小となるperplexityを設定します。
それではt-SNEの結果を出力してみましょう!
|
1 2 3 4 5 |
#================================== # 最適化したperplexityでt-SNEを学習 #================================== Z = TSNE(perplexity=optimal_perplexity, n_components=2, init='pca', random_state=random_state_number).fit_transform(df_X) |
|
1 |
data = pd.concat([df,pd.DataFrame(Z,columns=["Z1","Z2"])],axis=1) |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#====================================== # t-SNEで作成したケミカルディスタンスの可視化 #====================================== plt.figure(figsize=(6,5)) x = data["Z1"] y = data["Z2"] cmap_data = data["logS"] plt.scatter(x=x, y=y, c=cmap_data, marker=".",cmap="viridis",vmax=1,vmin=-11) plt.xlabel("Z1") plt.ylabel("Z2") plt.colorbar().set_label("logS") plt.show() |
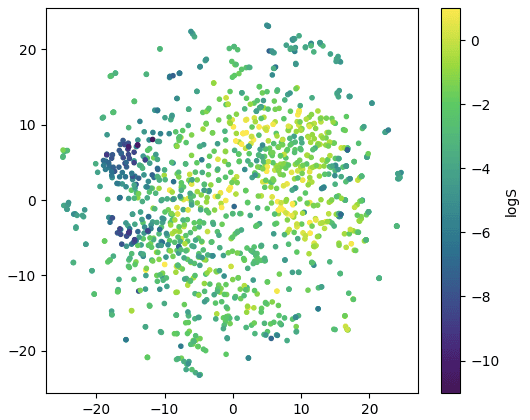
UMAPによる可視化
次にUMAPで次元削減を実装するコードを紹介します!
UMAPはハイパーパラメータチューニングがないのでシンプルです
|
1 2 3 |
# UMAPの適用 fit = umap.UMAP(random_state=42) u = fit.fit_transform(df_X) |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#====================================== # t-SNEで作成したケミカルディスタンスの可視化 #====================================== plt.figure(figsize=(6,5)) x = u[:, 0] y = u[:, 1] cmap_data = df["logS"] plt.scatter(x=x, y=y, c=cmap_data, marker=".",cmap="viridis",vmax=1,vmin=-11) plt.xlabel("UMAP1") plt.ylabel("UMAP2") plt.colorbar().set_label("logS") plt.show() |
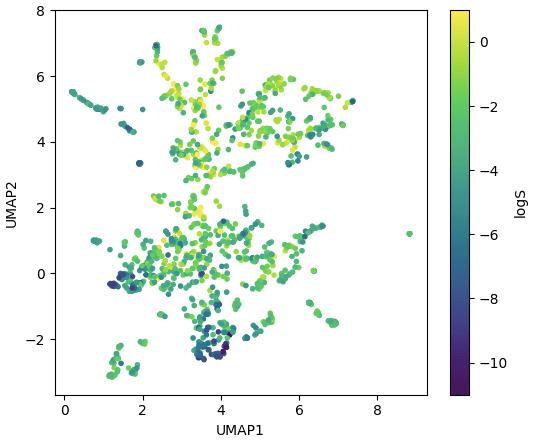
まとめ
UMAPとt-SNEの結果を比較すると、データのクラスタリングや分布の違いが見えてきます。
例えば、t-SNEでは全体的な円の構造を保ちつつ次元削減されています。
一方、UMAPでは、近いデータポイント間の関係が強調され、クラスタリングの詳細が明確に分かりやすいですね。
化学構造使ったデータ分析を行う際に、ぜひご活用下さい!!



コメント