こんにちはnissyです
前回に引き続き、化学構造を用いたデータ分析です!
化学構造と物理的性質との関係をモデリングする
定量的構造物性相関(QSPR、Quantitative Structure-Property Relationship)を用いて製品開発をサポーツするプロジェクトに参加することがありました。
私自信全く経験のない中、プロジェクトに参加させていただきインプットとアウトプットを自転車操業のように学んだ知識を紹介したいと思います。
私が活用したのはQSPRの解釈技術です。
ざっくりと説明すると、線形回帰分析やランダムフォレストでモデリング得られる特徴量重要度を化学構造に可視化する技術です。
それでは説明していきます!!!
Tanimoto-kernel 搭載 サポートベクター回帰
今回はTanimoto-kernelを用いたサポートベクター回帰でモデルを構築します。
Tanimoto-kernelは、フィンガープリントで表現された化学構造の類似度を測るために使用されるなカーネル関数です。
Tanimoto-kernelをSVRに組み込むことで、分子記述子間の類似度を高次元空間で利用し、
分子構造と物性間の非線形な関係をモデル化することが可能です。
Tanimoto-kernelを用いるSVRモデルの大きな特徴として、予測結果を個々のフィンガープリントの寄与に分解し、これによりどの構造が予測結果にどのような影響を与えているかを定量的に評価できます。
ライブラリーを読み込みます
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
import os import pandas as pd import numpy as np import matplotlib.figure as figure import matplotlib.pyplot as plt from rdkit import Chem from rdkit.Chem import AllChem, Draw from rdkit.Chem.Draw import rdMolDraw2D from IPython.display import SVG, display from sklearn import svm from dcekit.variable_selection import search_high_rate_of_same_values, search_highly_correlated_variables from sklearn.model_selection import train_test_split,GridSearchCV import requests import glob from rdkit.Chem import AllChem from sklearn.metrics.pairwise import pairwise_distances from sklearn.base import BaseEstimator, RegressorMixin, ClassifierMixin from sklearn.svm import SVR from sklearn.metrics.pairwise import pairwise_kernels from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error from sklearn.metrics import jaccard_score import time |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# ======================= # データセットの読み込み # ======================= df = pd.read_csv('SMILES_logS_データセット.csv') # ======================= # 学習に時間がかかるので、ランダムにサンプルを抽出 # ======================= df = df.sample(n=50, random_state=42) # ============================ # 目的変数を中心化 標準化すると学習が弱くなる # ============================ y_name = 'logS' y = df[y_name] y_ave = y.mean() y_std = y.std() autscaled_y = (y-y_ave) #================================ # SMILES⇒ECFP4への変換 ビットを大きくしないと結合部はハイライトされにくい #================================ radius= 2 bit =8192 #2^n (n=正の整数)の値を設定すること。フィンガープリントが二進数記法なので mols_list = [Chem.MolFromSmiles(smiles) for smiles in df["SMILES"]] ECFP = [AllChem.GetMorganFingerprintAsBitVect(mol, radius,bit) for mol in mols_list] df_X = pd.DataFrame(np.array(ECFP, int)) |
まずTanimoto-kernelの関数を設定します。これはジャッカード距離と同じ概念です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
#============== # タニモトカーネルの関数の設定(ジャッカード距離) #============== def tanimoto_kernel(X, Y=None): """ カスタムカーネル関数。ジャッカード類似度行列を計算する。 Parameters: X (pd.DataFrame or np.ndarray): サンプルデータ Y (pd.DataFrame or np.ndarray, optional): サンプルデータ。指定しない場合はXを使用します。 Returns: np.ndarray: ジャッカード類似度行列 """ if isinstance(X, pd.DataFrame): X = X.values if Y is None: Y = X elif isinstance(Y, pd.DataFrame): Y = Y.values num_samples_X = X.shape[0] num_samples_Y = Y.shape[0] similarity_matrix = np.zeros((num_samples_X, num_samples_Y)) for i in range(num_samples_X): for j in range(num_samples_Y): similarity_matrix[i, j] = jaccard_score(X[i], Y[j]) return similarity_matrix |
Tanimoto-kernel搭載したサポートベクター回帰の学習を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# ========================================================= #クロスバリデーションで、SVRのハイパーパラメータを最適化(100サンプルで5分) # ========================================================= # ハイパーパラメータの最適値を探索 params = {'C':2 ** np.arange(-5, 5, 3, dtype=float), 'epsilon':2 ** np.arange(-10, 0, 3, dtype=float) } model_cv = GridSearchCV(svm.SVR(kernel=tanimoto_kernel), params,cv=5, n_jobs=-1) model_cv.fit(df_X, autscaled_y) # ハイパーパラメータの最適値を設定 model = svm.SVR(kernel=tanimoto_kernel, C=model_cv.best_params_['C'], epsilon=model_cv.best_params_['epsilon']) # モデルの学習 model.fit(df_X, autscaled_y) |
学習結果を確認してみます
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# ================================================================== # トレーニングデータの予測 # ================================================================== autscaled_predicted_y = model.predict(df_X) predicted_y = autscaled_predicted_y + y_ave plt.figure(figsize=(5,5)) plt.scatter(y.values, predicted_y , c="blue",alpha=0.5,label="Train") plt.plot([-60,200],[-60,200],"k",linestyle="dashed",linewidth = 0.8) #対角線の表示 plt.xlim(-10,5) #横軸の幅 plt.ylim(-10,5) #縦軸の幅 plt.xlabel("Actual "+y_name) plt.ylabel("Predicted "+y_name) print('r^2 for test data :', r2_score(y , predicted_y)) print('RMSE for test data :', mean_squared_error(y , predicted_y, squared=False)) print('MAE for test data :', mean_absolute_error(y , predicted_y)) plt.show() |
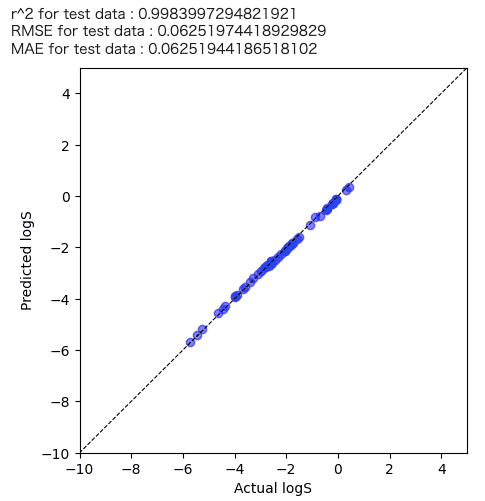
この時、決定係数R2が低いと構造物性相関が取れていないということになります。
R2が低くなった場合の考えられる要因として、化学構造以外の特徴量が物性に対する寄与が大きい等が考えられます。
今回のケースではlogSは化学構造の寄与が大きいため上記のような結果が得られたと考えられます。
続いて、この学習結果を元に化学構造へのハイライトを行なっていきます!
次に化学構造が目的変数へ与えている寄与度を、個々のフィンガープリントの寄与に分解し、それらを抽出します。式については論文を参考しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
support_vectors = model.support_ dual_coefs = model.dual_coef_ # サポートベクターのインデックス取得 support_indices = model.support_ # サポートベクターとして選ばれなかったサンプルのインデックス取得 all_indices = np.arange(df_X.shape[0]) non_support_indices = np.setdiff1d(all_indices, support_indices) V = df_X.drop(non_support_indices) dual_coefs = model.dual_coef_ va = dual_coefs.T*V sigma_v = V.sum(axis=1) Feature_Weight = ((va.T/sigma_v.T).T).sum() |
各フィンガープリントに与えられた寄与度は以下のコードで確認できます。
|
1 2 3 |
selected_bit_num = Feature_Weight.index bit_coef = dict(zip(selected_bit_num, Feature_Weight.values)) bit_coef |

それでは化学構造にハイライトさせて行きましょう!!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 |
for num in range(len(df)): conf = 1 radius = 2 bit = 8192 mols_list = [Chem.MolFromSmiles(smiles) for smiles in df["SMILES"]] mol = mols_list[num] print(y_name , y.iloc[num]) print("Predicted value: {:.3f}".format(predicted_y[num])) bitI_morgan = {} fp_morgan = AllChem.GetMorganFingerprintAsBitVect(mol, radius, bit, bitInfo=bitI_morgan) bit_list = list(set(selected_bit_num) & set(bitI_morgan.keys())) Ai_list = np.zeros(mol.GetNumAtoms()) highlight_bonds = [] atoms = [] atom_colors = {} bonds_colors = {} for bit in bit_list: atom_idx, radius = bitI_morgan[bit][0] env = Chem.FindAtomEnvironmentOfRadiusN(mol, radius, atom_idx) highlight_bonds.extend(env) bond_list = np.zeros(mol.GetNumBonds()) # 対象の結合に対して寄与度を振り分け for bit in bit_list: Cn_1 = bit_coef[bit] fn_1 = len(bitI_morgan[bit]) for part in bitI_morgan[bit]: if part[1] == 0: i = part[0] if i < len(bond_list): xn_1 = 1 bond_list[i] += Cn_1 / fn_1 / xn_1 else: amap = {} env = Chem.FindAtomEnvironmentOfRadiusN(mol, radius=part[1], rootedAtAtom=part[0]) submol = Chem.PathToSubmol(mol, env, atomMap=amap) xn_1 = len(list(amap.keys())) for i in env: if i < len(bond_list): bond_list[i] += Cn_1 / fn_1 / xn_1 # 対象の原子に対して寄与度を振り分け for bit in bit_list: Cn = bit_coef[bit] fn = len(bitI_morgan[bit]) for part in bitI_morgan[bit]: if part[1] == 0: i = part[0] if i < len(Ai_list): xn = 1 Ai_list[i] += Cn / fn / xn else: amap = {} env = Chem.FindAtomEnvironmentOfRadiusN(mol, radius=part[1], rootedAtAtom=part[0]) submol = Chem.PathToSubmol(mol, env, atomMap=amap) xn = len(list(amap.keys())) for i in amap.keys(): if i < len(Ai_list): Ai_list[i] += Cn / fn / xn # Ai_list = Ai_list / 1.5 Ai_list = Ai_list*conf # ハイライトする原子と色,円の半径を設定 atoms = [i for i in range(len(Ai_list))] atom_colors = dict() for i in atoms: if Ai_list[i] > 0: atom_colors[i] = (1, 1 - Ai_list[i], 1 - Ai_list[i]) else: atom_colors[i] = (1 + Ai_list[i], 1 + Ai_list[i], 1) # bond_list = bond_list/ 1.5 bond_list = bond_list*conf bonds = [i for i in range(len(bond_list))] bonds_colors = dict() for i in bonds: if bond_list[i] > 0: bonds_colors[i] = (1, 1 - bond_list[i], 1 - bond_list[i]) else: bonds_colors[i] = (1 + bond_list[i], 1 + bond_list[i], 1) # コンテナの準備 view = rdMolDraw2D.MolDraw2DSVG(300, 350) tm = rdMolDraw2D.PrepareMolForDrawing(mol) view.DrawMolecule(tm, highlightAtoms=atoms, highlightAtomColors=atom_colors, highlightBonds=highlight_bonds, highlightBondColors=bonds_colors) view.FinishDrawing() svg = view.GetDrawingText() display(SVG(svg)) # SVGを表示 |
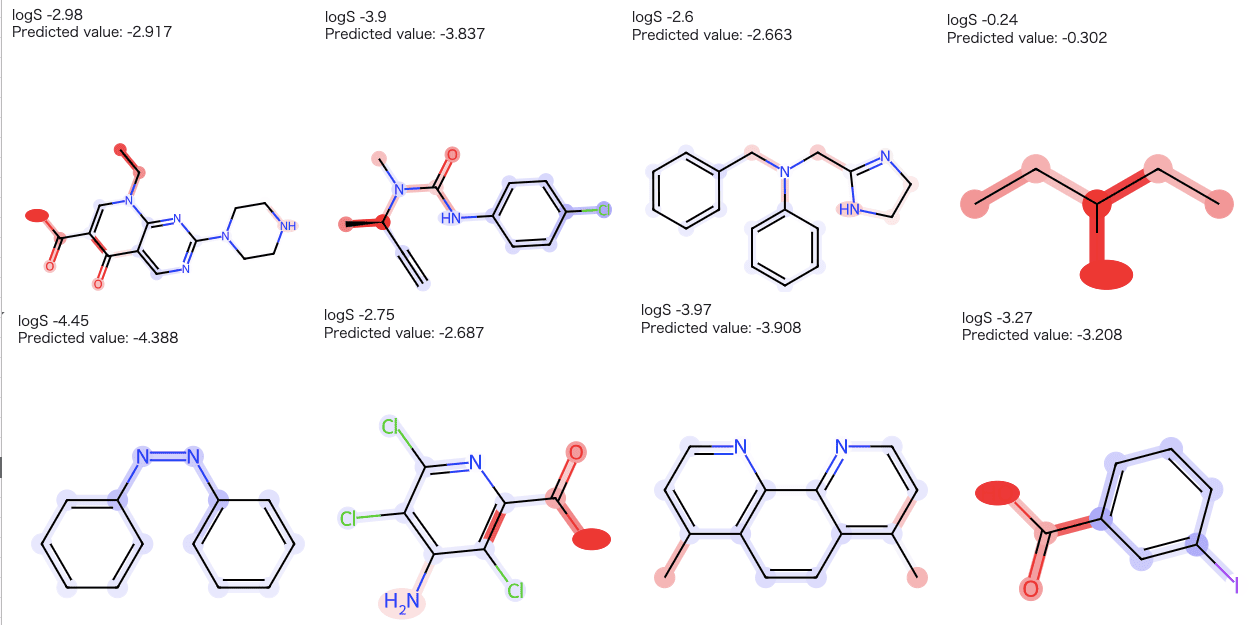
まとめ
Tanimoto-kernelを搭載したサポートベクター回帰は、特に分子構造の類似性を考慮した予測において解釈性の高さから、材料設計分野での活用が期待されます。一方で、計算コストやパラメータ調整などのコツも必要になるため、データに応じてトライアル&エラーを繰り返して実装してみてください!
Tanimoto-kernelを搭載したサポートベクター回帰はマーケティング分析とかにも使えいそうな気がする・・・
参考文献
R.Asahara, T.Miyao, ACS Omega, 7, 26952(2022).
R.Rodríguez-Pérez, M.Vogt, J.Bajorath、ACS Omega, 2, 6371(2017).



コメント