こんにちは、nissyです。
本日は”主成分分析“について解説したいと思います。
主成分分析は”教師なし学習”である次元削減手法の一つです。
次元削減と聞いて「難しそう」と思ったそこのあなた・・・大丈夫です!!重回帰分析を理解した方なら主成分分析も理解できます。
次元削減とは
次元削減とは”教師なし学習”の1つで、データセットの特徴量の次元を削減する手法です。
不要な特徴量を削除する特徴量選択とは異なり、元の特徴量の有する情報量を可能な限り損なわず、少数の新しい特徴量(主成分)を作り出すことを目的とします。
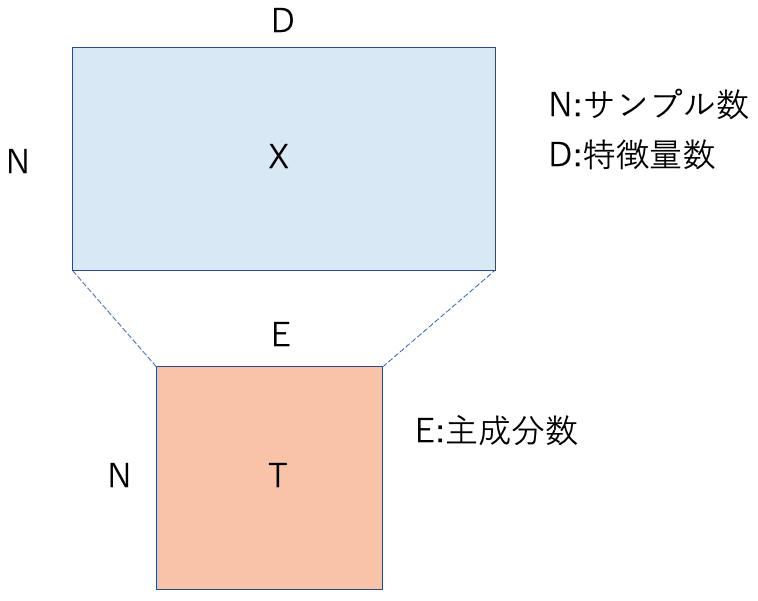
データセットの次元削減をすることで、以下のメリットが得られます。
- 高次元データをグラフ化し、解釈する事ができる
- 高次元データの機械学習計算コストを下げる事ができる。
高次元データというのは単純に特徴量の多いデータセットを意味しますが、化学系でよく扱うのはIR、XRDなどの構造規定するためのスペクトルデータや、製造プロセスにおける時系列データも該当します。
【スペクトルデータの主成分分析のイメージ】
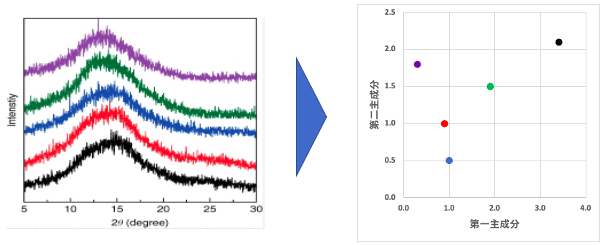
スペクトルデータを散布図に写すことのメリットは予想以上に大きいです。例えば、高分子の物性値をX軸にとってスペクトルの主成分をY軸に取る事で、物性と構造の関係性を確認する事ができます。
現状主成分がスペクトルのどの情報を圧縮しているのかは不明ですが、主成分の解釈についても後述します。
主成分分析について
主成分分析の流れ
主成分分析はデータの主成分となる軸を探し、その軸にデータを写像して次元を圧縮する線形の次元削減手法になります。
情報科学の分野ではデータセットのばらつきが大きいほど情報量が多いと考えます。すでに知っているデータよりも「未知のデータ」の方が得られる情報量が多い、ということです。情報量を多く含んでいるデータセットほど個体差が現れやすく、機械学習により多くの知見を与える事ができます。
主成分分析は以下のような流れで主成分となる軸を探索していきます。
- まずデータの分散が最大となる方向を第一主成分とする。
- 次に、第一主成分に直行する方向で分散が最大化される軸を、第二主成分とする。
- 次に、第二主成分に直行する方向で分散が最大化される軸を、第三主成分とする。
- 以下、2,3を繰り返し。
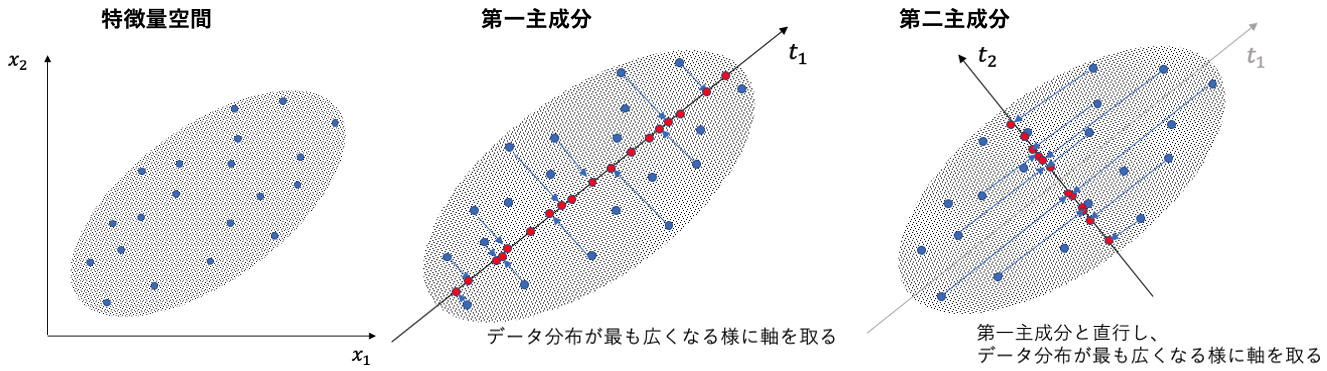
直行する方向でというのは非常に大事な概念ですので覚えておきましょう。
主成分分析は 重回帰分析の”教師なし学習版”
以上の説明でイメージがつきにくい方は式で覚えてしまうことをおすすめします。第一主成分の式は以下の通りになります。$$\boldsymbol{t_1}=p_1^{(1)}\boldsymbol{x_1}+p_2^{(1)}\boldsymbol{x_2}+…$$
\(\boldsymbol{x_1}\)、\(\boldsymbol{x_1}\)は特徴量ベクトルです。データセットの赤枠部分に対応します。
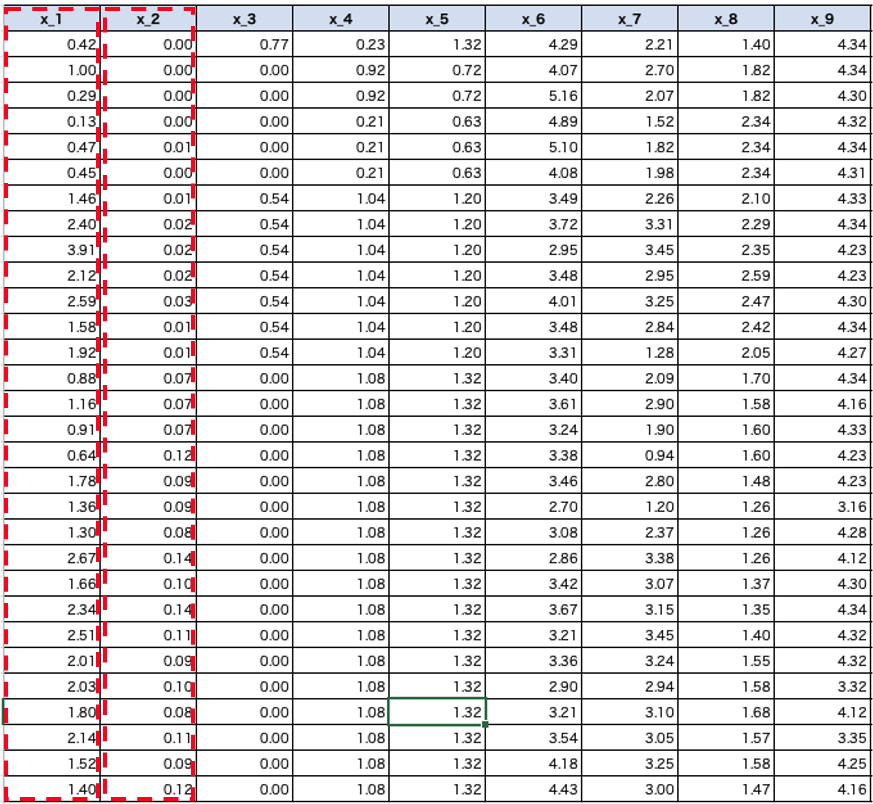
上記の式は重回帰分析の式と同じに見えますよね。この\(\boldsymbol{t_1}\)を第一主成分スコアと言います。先ほどXRDのスペクトルデータを散布図に移した際の、散布図のデータはこの主成分スコアの値を使っています。
主成分分析で機械学習により最適化されるパラメータは\(p_1^{(1)}\)、\(p_2^{(1)}\)…です。重回帰分析での回帰係数に相当する\(p_1^{(1)}\)、\(p_2^{(1)}\)…のことをローディングと言います。
重回帰分析は”教師あり学習”でしたので、「yの実測値」と「yの予測値」の二乗誤差を評価指標とし、二乗誤差の値が最小になる様にパラメータ(回帰係数)を最適化すれば良いのでした。
ただし主成分分析は”教師なし学習”ですので二乗誤差のような評価指標はありません。評価指標を明確にしていないので機械学習はパラメータ(ローディング)の最適化を行う事ができません。それでは、どの様な評価指標を立ててあげれば良いでしょうか・・・??
答えは、”データの分散”です。
データの分散が最大となる様な軸を取ってあげれば良いのでした。
パラメータの最適化方法は初学者にとってはアドバンスな内容になります。まだ理解が追いついていないという方はひとまず「分散が最大になるようにパラメータ(ローディング)を最適化する」と覚えていただければ大丈夫です。
主成分分析のパラメータ最適化は”Lagrange の未定乗数法”という手法を使います。これはある制約条件(範囲)の中でパラメータを最適化します。

「範囲を決める、指標を立てる、パラメータを最適化する」
ここでも”範囲”が出てきましたね
今回の制約条件(範囲)は、$$(p_1^{(1)}) ^2+(p_2^{(1)}) ^2+…+(p_n^{(1)}) ^2=1$$です。またデータの分散を最大化させることは、全てのサンプルの主成分スコアの二乗和を最大化させることに対応します。数式にするといかの最適化問題を解くことに相当します。
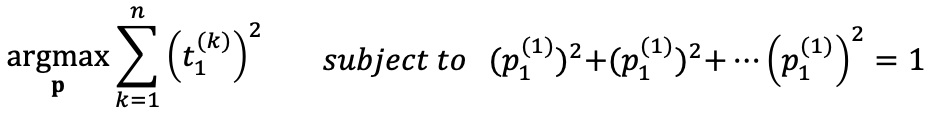

<人の役割部分>をまとめると、
範囲が \((p_1) ^2+(p_2) ^2+…+(p_n) ^2=1\)
評価指標は”データの分散”になりますね。
機械学習を行う上での<人の役割>については以下の記事で紹介しています。

第二主成分以降は一つ前の主成分軸に直行するという条件が追加されますが、それ以外は第一主成分を求める時と同じ条件でパラメータを最適化します。
Pythonで主成分分析を実装
データセットの確認、主成分分析の実装
それでは実際にPythonを使って「Irisデータセット」を主成分分析していきます。
まずは使用するライブラリーをインポートします。
|
1 2 3 4 5 6 7 8 |
import numpy as np import pandas as pd import matplotlib.pyplot as plt import sklearn from sklearn.decomposition import PCA import seaborn as sns from sklearn.datasets import load_iris #Irisデータセット import matplotlib.patches as patches |
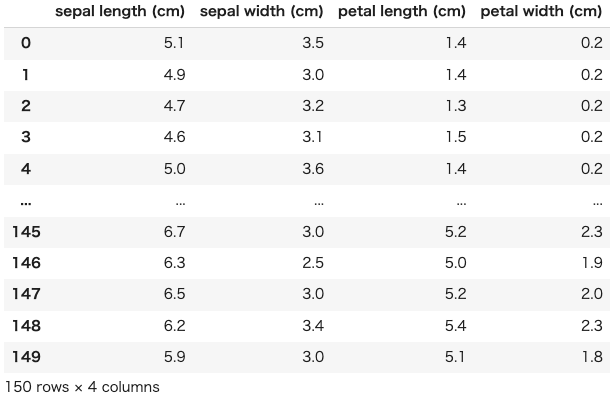
次にIrisデータセットを用意します。実務の状況に近づけるためにデータフレームの形でデータセットを確認します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#=================== # データセットの読み込み #=================== iris_data = load_iris() X = iris_data['data'] y = iris_data['target'] feature_names = iris_data['feature_names'] target_names = iris_data['target_names'] #=================== # 説明変数 #=================== X = pd.DataFrame(X) X.columns=feature_names #カラムに名前をつけている。 #=================== # 目的変数 #=================== y = pd.DataFrame(y) #=================== # 説明変数と目的変数の結合 #=================== df = X.join(y) df = df.rename(columns={0:"target_names"}) |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#=================== # ペアプロット図の出力 #=================== sns.pairplot(df,hue="target_names",palette='viridis') #=================== # 相関行列の出力 #=================== plt.rcParams["font.size"] = 10 df_corr_of_pcs_space_X = X.corr() plt.figure(figsize=(8,6)) sns.heatmap(df_corr_of_pcs_space_X.iloc[:20,:20], annot=True, cmap="RdBu") |
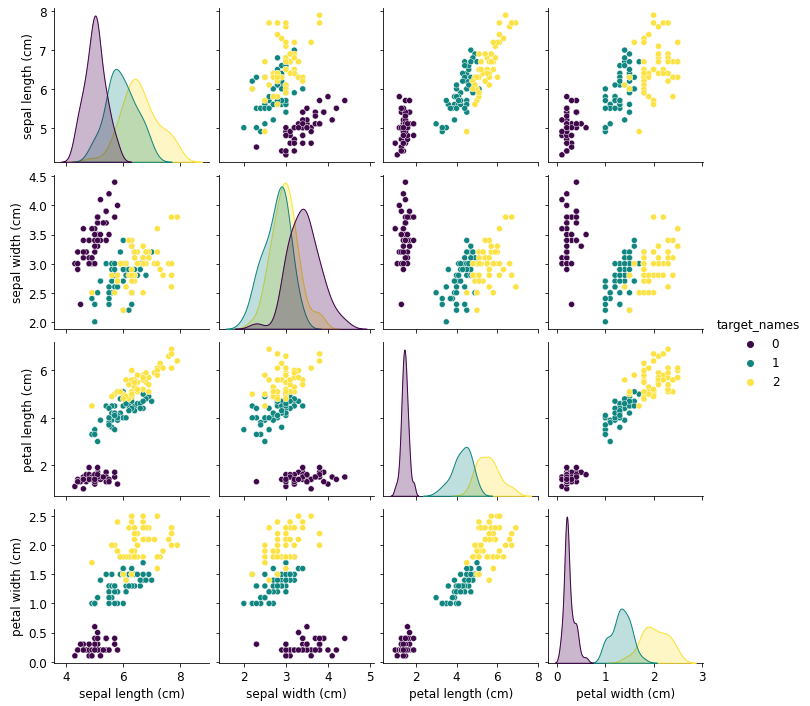
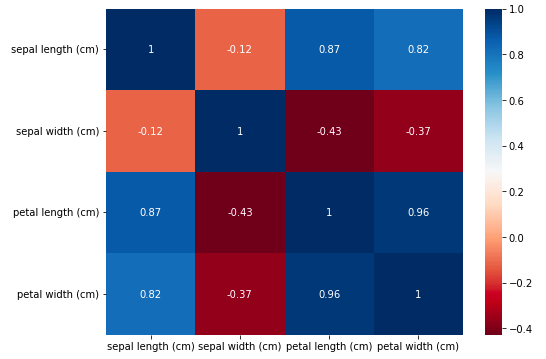
“sepal length (cm)”、”petal length (cm)”、”petal width (cm)”で相関の有するデータセットである事が確認できます。
それでは主成分分析を実装していきましょう。以下のコードを走らせれば主成分分析の実装が完了します。
|
1 2 3 4 5 6 7 |
#=================== # データセットの標準化 #================== autoscaled_X = (X - X.mean())/X.std() pca = PCA(n_components=4) #モデルの宣言 pca.fit(autoscaled_X) #モデルの学習 |
主成分分析の結果を解釈する
所有しているデータセットに対して主成分分析を実装させた後、学習させたモデルから以下の情報を抽出していきます。
- 主成分スコア
- 累積寄与率
- ローディング
主成分スコア
主成分スコアは以下のコードで取得できます。
|
1 2 3 4 5 |
#主成分スコアの取得 pca_score_X=pca.transform(autoscaled_X) #データフレームの形に変換 range()の中は主成分の数を入れる df_pca_score_X = pd.DataFrame(pca_score_X, columns=["PC{}".format(x + 1) for x in range(4)]) |
出力すると以下のようなデータフレームが得られている事が確認できます。
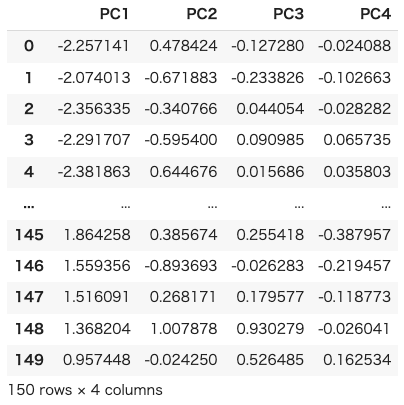
ここで主成分の軸の取り方についておさらいしておきます。
- まずデータの分散が最大となる方向を第一主成分とする。
- 次に、第一主成分に直行する方向で分散が最大化される軸を、第二主成分とする。
- 次に、第二主成分に直行する方向で分散が最大化される軸を、第三主成分とする。
- 以下、繰り返し。
各主成分軸は直行するように選ばれているはずなので、主成分軸に描写された主成分スコアは無相関になるはずです。相関行列を出力させて確認してみましょう。
|
1 2 3 4 5 6 7 8 9 |
#ペアプロット図を出力 df_pca = df_pca_score_X.join(y) sns.pairplot(df_pca,hue="target_names",palette='viridis') #相関行列を出力 plt.rcParams["font.size"] = 10 df_corr_of_pcs_space_X = df_pca_score_X.corr() plt.figure(figsize=(8,6)) sns.heatmap(df_corr_of_pcs_space_X.iloc[:20,:20], annot=True, cmap="RdBu") |
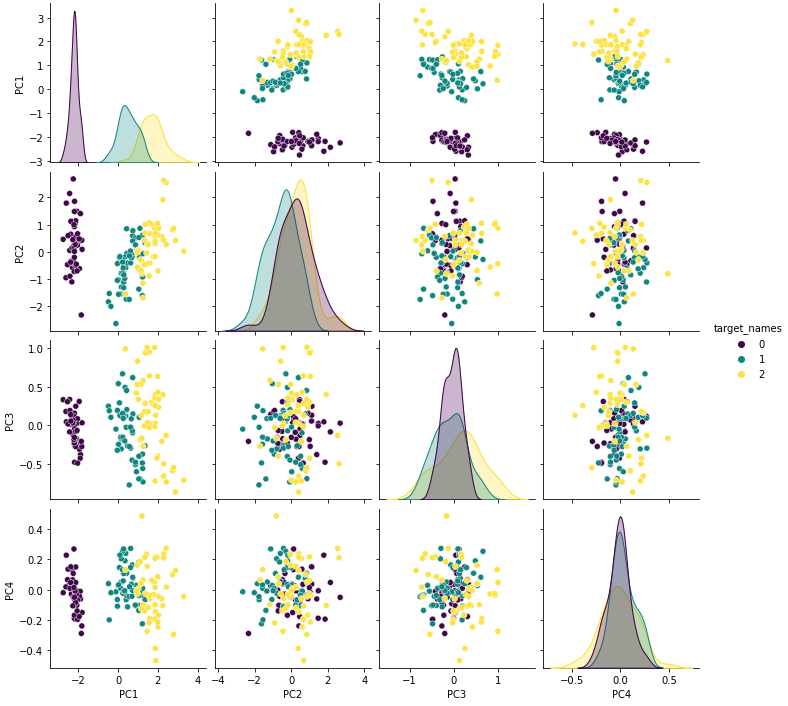
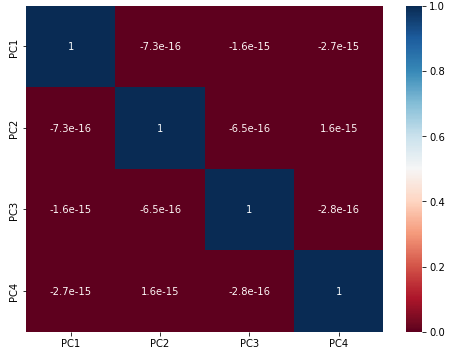
上図より非対角成分の相関係数がほぼ0となっており、各主成分間で無相関になっている事が確認できました。
この特徴のメリットとして、主成分分析をデータの前処理として行えば多重共線性を回避する事ができます。
寄与率、累積寄与率
主成分分析では元のデータセットの情報量をどれだけ各主成分が保持できているかを確認する事ができます。まずは以下のコードで寄与率と累積寄与率のグラフを出力してみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
#=================== # 累積寄与率の計算 #=================== contribution_ratio=pca.explained_variance_ratio_ #寄与率を求める cumulative_contribution_ratio=[] contribution_ratio_sum=0 for i in list(contribution_ratio): contribution_ratio_sum+=i cumulative_contribution_ratio.append(contribution_ratio_sum) #=================== # グラフの表示 #=================== plt.figure(figsize=(6,4)) plt.bar(np.arange(1,len(cumulative_contribution_ratio)+1),contribution_ratio) plt.scatter(np.arange(1,len(cumulative_contribution_ratio)+1),cumulative_contribution_ratio,color='red') plt.plot(np.arange(1,len(cumulative_contribution_ratio)+1),cumulative_contribution_ratio,color='red') plt.xticks(np.arange(1,len(cumulative_contribution_ratio)+1)) plt.xlabel('PCA') plt.ylabel('Cumulative contribution ratio') plt.show() |
上のコード走らせると以下のグラフを得る事ができます。まずはグラフの見方について説明します。
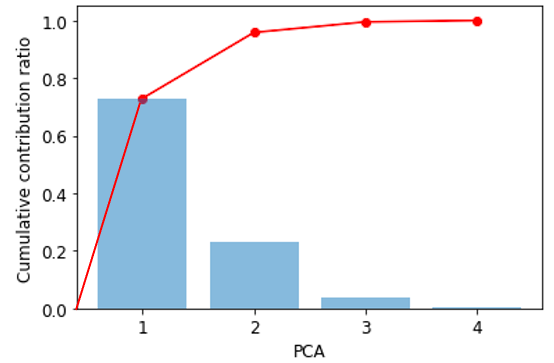
棒グラフは各主成分の寄与率を示しています。言い換えると、各主成分が保持している元のデータセットの情報量の割合です。
例えば、「上図より第一主成分(PC1)に約70%以上の情報が保持されている事が確認できた」という事が言えます。
赤で示している折れ線グラフは累積寄与率を示しています。今回のデータセットでは「PC1とPC2だけで90%以上の情報を保持している」事が言えます。
上記より、情報量を可能な限り損なわず新しい特徴量を作る事ができ、また2つの主成分だけで元のデータの9割以上を保持していることが明らかとなりました。

各主成分の寄与率はどうやって決まるんですか?

非常に良い質問です。詳しく説明します。
結論として、寄与率は主成分分析後の”データの分散”から算出します。
主成分分析前後でのデータセットについて確認してみましょう!
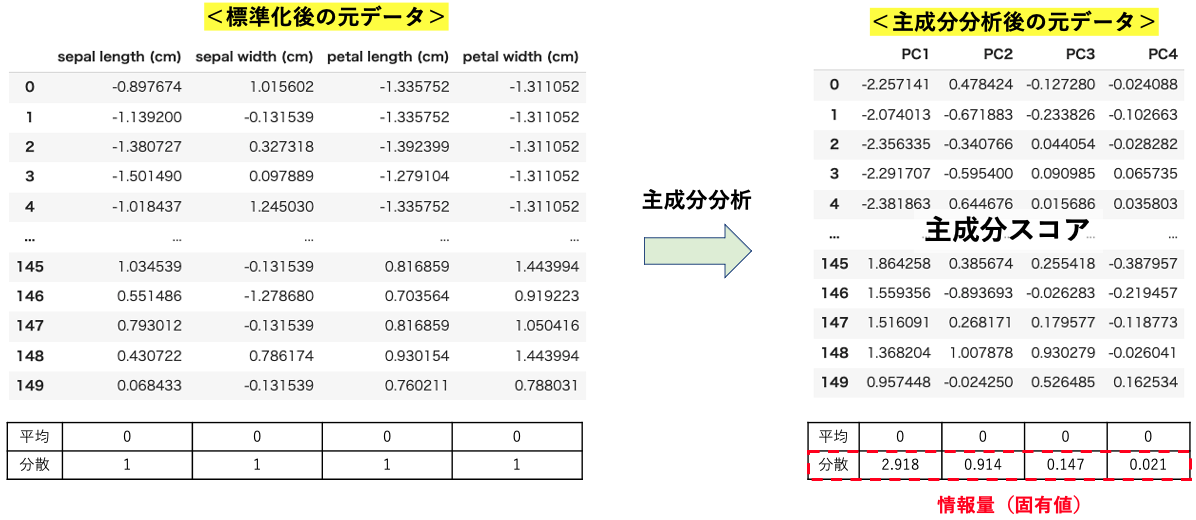
このように主成分分析後に得られた主成分スコアの分散を情報量として用います。
このことから、例えばPC1の寄与率は$$\frac{2.918}{2.918+0.914+0.147+0.021}\simeq0.725$$のように求める事ができます。

元のデータセットの情報量も分散の大きさで評価したのと同様に、主成分分析後の情報量も分散の大きさで評価します。
ローディング
主成分スコアは主成分分析のアルゴリズムに基づいて算出されたただの数値ですが、できるだけ主成分の持っている情報を適切に言語化する事で分析結果の価値を上げる事が求められます。
そのために、主成分分析を実装する上で学習データより最適化したパラメータであるローディングを確認していきましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# ローディング plt.figure(figsize=(6,4)) plt.rcParams["font.size"] = 12 PC1 = pca.components_[0] PC2 = pca.components_[1] PC3 = pca.components_[2] PC4 = pca.components_[3] plt.plot(PC1,label="PC1") plt.plot(PC2,label="PC2") plt.plot(PC3,label="PC3") plt.plot(PC4,label="PC4") plt.ylim(-1,1) # plt.xticks([feature_names]) plt.xticks([0, 1,2,3],feature_names,rotation=10) plt.legend(ncol=4,loc="best") plt.show() |
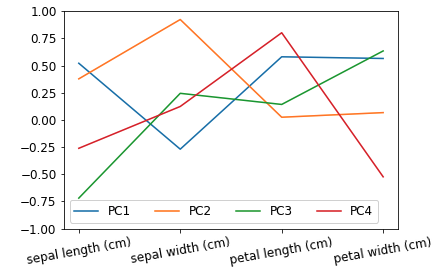
水色線のPC1に着目します。
PC1は”sepal length (cm)”、”petal length (cm)”、”petal width (cm)”に対して0.50程度のローディングを持っています。
一方で”sepal width (cm)”に対してのみ-0.25程度のローディングとなっています。
つまりPC1の大きいサンプルは”sepal length (cm)”、”petal length (cm)”、”petal width (cm)”の値が大きく、”sepal width (cm)”の値が小さいサンプルである事がわかります。
次にバイプロットという可視化方法を実装してみます。
バイプロットとは主成分分析による次元圧縮前の空間の各特徴が次元圧縮後の空間でどの方向を指しているかを可視化する方法です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
plt.figure(figsize=(6,6)) magnification = 2.5 # 矢印の倍率 #散布図 sns.scatterplot(data=df_pca, x="PC1", y="PC2", hue="target_names",palette='viridis') #ベクトル1 plt.arrow(0,0,PC1[0]*magnification ,PC2[0]*magnification , color='r',width=0.0005,head_width=0.05,alpha=0.5) plt.text(PC1[0]*magnification, PC2[0]*magnification+0.2, "sepal length (cm)", color='r') #ベクトル2 plt.arrow(0,0,PC1[1]*magnification ,PC2[1]*magnification , color='r',width=0.0005,head_width=0.05,alpha=0.5) plt.text(PC1[1]*magnification+0.3, PC2[1]*magnification+0.2, "sepal width (cm)", color='r') #ベクトル3 plt.arrow(0,0,PC1[2]*magnification ,PC2[2]*magnification , color='r',width=0.0005,head_width=0.05,alpha=0.5) plt.text(PC1[2]*magnification+0.2, PC2[2]*magnification-0.1, "petal length (cm)", color='r') #ベクトル4 plt.arrow(0,0,PC1[3]*magnification ,PC2[3]*magnification , color='r',width=0.0005,head_width=0.05,alpha=0.5) plt.text(PC1[3]*magnification, PC2[3]*magnification+0.1, "petal width (cm)", color='r') plt.xlabel("PC1") plt.ylabel("PC2") plt.show() |
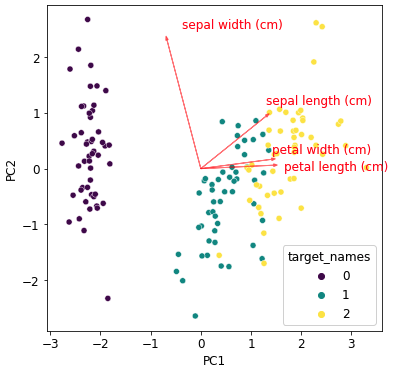
例えば”sepal width”のベクトルは散布図の左上をさせていますが、これは”sepal width”の値が大きいサンプルは散布図の左上に位置していることを示しています。

この矢印はどのように引かれているのですか?

またまた良い質問ですね。もちろん説明します。
今回のirsデータセットの場合、第一主成分および第二主成分は以下の式より計算されています。
$$\boldsymbol{t_1}=p_{sl}^{(1)}\boldsymbol{x_{sl}}+p_{sw}^{(1)}\boldsymbol{x_{sw}}+p_{pl}^{(1)}\boldsymbol{x_{pl}}+p_{pw}^{(1)}\boldsymbol{x_{pw}}$$
$$\boldsymbol{t_2}=p_{sl}^{(2)}\boldsymbol{x_{sl}}+p_{sw}^{(2)}\boldsymbol{x_{sw}}+p_{pl}^{(2)}\boldsymbol{x_{pl}}+p_{pw}^{(2)}\boldsymbol{x_{pw}}$$
例えば”petal width (cm)”のベクトルは始点(0,0)から(\(p_{pw}^{(1)}\),\(p_{pw}^{(2)}\))への矢印を描写しています。
それに加え、今回は散布図に対してベクトルの大きさが小さかったので、ベクトルを主張させるために全てのベクトルに対してPC1、PC2方向に2.5倍しています。
最後にローディングの制約条件\((p_1^{(1)})^2+(p_2^{(1)})^2+…+(p_n^{(1)})^2=1\)が満たされているかを確認してみましょう。
|
1 2 |
#第一主成分のローディングの二乗和を計算 pca.components_[0][0])**2+pca.components_[0][1]**2+pca.components_[0][2]**2+pca.components_[0][3]**2 |
上記コードを走らせると”1.0000000000000007”の値が出力されます。制約条件が満たされていることも確認できました。
実務ではこのような情報を整理して、専門的な知識と結びつけて各々の主成分が持つ意味を言語化するようにしてください。
まとめ
今回は主成分分析について解説いたしました。
主成分分析は解釈性の高い次元削減手法であり、次元削減後のデータをある分野の専門知識と結びつける事も可能です。
この記事を参考にぜひ実務でも主成分分析を使用していただければと思います。
主成分分析の数理的な解説はできるだけ省いて記事としてまとめましたので、もっと深く主成分分析を学びたいと思った方は”固有値問題”、”対角化”、”特異値分解”といったキーワードを加えて主成分分析について調べてみてください。


コメント