こんにちは、nissyです。
今日は「決定木回帰分析」について説明します。
決定木とは、データを分類するための構造を作り出すシンプルで直感的な手法です。
「決定木回帰分析」は、データの複雑なパターンを捉えつつ、その結果を人間が理解しやすい形で提示する強力な手法と言えます。
このブログでは、決定木の基本的な概念を紐解きながら、どのような利点を持っているのかを理解していただくことを目指しています。
決定木の基礎
決定木は、その名の通り木の形をしていて、データの特徴と目的変数との関係を表現します。この「木」はノード(Node)とエッジ(Edge)という二つの主要な要素から成り立ちます。
ノードはデータの特徴を表現し、エッジはその特徴に対する条件、すなわち分岐を表します。
最初のノードであるルートノードから始まり、特徴の条件に従って枝分かれし、最終的に葉ノード(Leaf Node)で予測結果が出力されます。
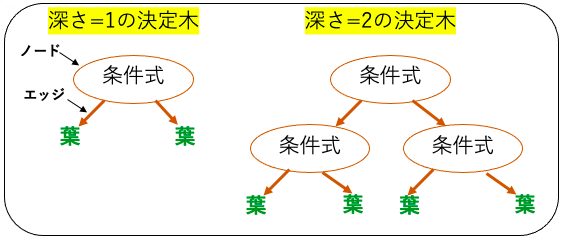
決定木はルールベースのモデルであり、データセットの特徴と目的変数の関係を最もよく表現するルール(分岐条件)を探索します。それ故に、最適化されたモデルを人間でも解釈できる事が大きな利点です。
決定木アルゴリズムの学習の流れは以下のようになります。
- 対象となる特徴量を1つ選択する
- 閾値候補を作成(計算)する
- 評価関数に基づき閾値候補の中から最適な閾値を選択する
- 1〜3を繰り返し、決定係数やRMSEを基に最適な木の深さを決定する

また決定木は、非線形な関係性を表現することが可能です。
これは、決定木が特徴空間をルールに基づいて分割し、各領域で独立に予測を行うためです。
この方式により、複雑なパターンや非直線的な関係性をモデルに組み込むことが可能になります。
一方で、決定木は深く成長させると訓練データのノイズに対してルールを適合してしまうため、過学習に陥りやすいと言われます。
決定木回帰分析を行うときは、これらの利点と欠点を考慮しつつ使用する必要があります。
Pythonで決定木回帰分析を実装
今回も「ボストン住宅価格データセット」を用いて「決定木回帰分析」を行っていきます。
まずは使用するライブラリーをインポートします。
|
1 2 3 4 5 6 7 8 |
import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.tree import DecisionTreeRegressor, export_graphviz # 決定木の構築に使用 from sklearn.model_selection import train_test_split, KFold, cross_val_predict from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error import graphviz import seaborn as sns |
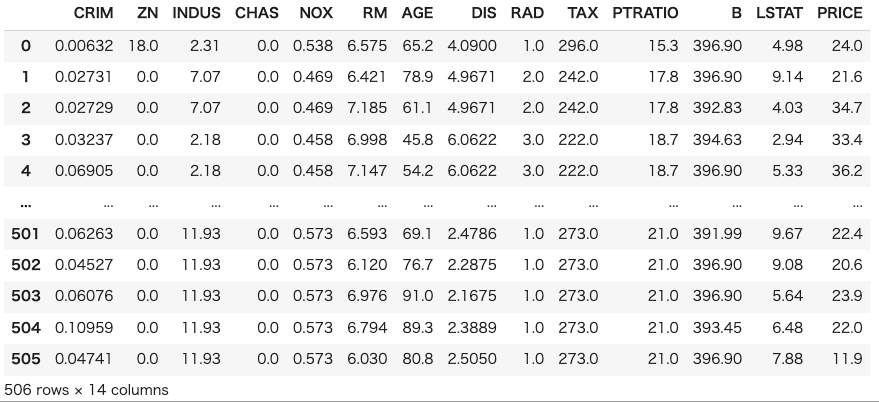
次にボストン住宅価格データセットを用意します。実務の状況に近づけるためにデータフレームの形でデータセットを確認します。
|
1 2 3 4 5 6 7 8 |
data_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data" column_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'PRICE' ] df = pd.read_csv(data_url, header=None, delim_whitespace=True, names=column_names) # データセットの表示 df |
以下のコードでデータを学習データとテストデータに分割します。決定木はルールベースのモデルなので、正規化は不要です。
|
1 2 3 4 5 6 |
#================================== # データを学習データとテストデータに分割する #================================== X = df.iloc[:,:-1] y = df["MEDV"] x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) |
学習曲線
決定木アルゴリズムを最適化するための主なハイパーパラメータは以下の4つです。
| max_depth | 決定木の最大の深さを指定する。深さが深いほどモデルは複雑になり、過学習になる可能性が高くなる。一方で、深さが浅いとモデルは単純になり、未学習(underfitting)になる可能性が高くなる。 |
| min_samples_leaf | リーフノード(決定木の末端のノード)に必要な最小のサンプル数。min_samples_leafの値が大きいほどモデルは単純になり、過学習を防ぐことができる(バリアンスが低くなり、バイアスが高くなる)。しかし、値が大きすぎるとモデルが単純すぎてデータのパターンを捉えられなくなります。 |
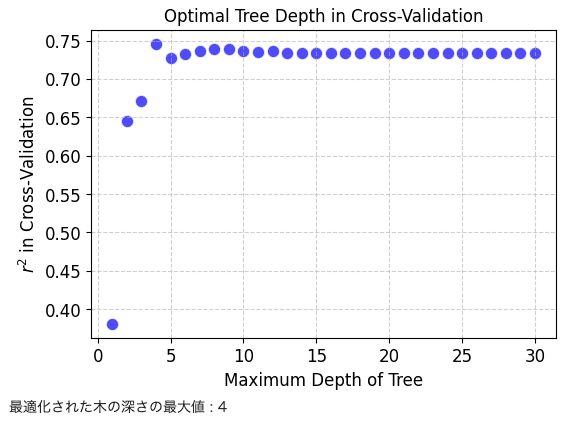
以下でクロスバリデーションを用いて、max_depthの最適化を行います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
fold_number = 10 # クロスバリデーションの fold 数 max_depths = np.arange(1, 31) # 木の深さの最大値の候補 min_samples_leaf = 3 # 葉ノードごとのサンプル数の最小値 # 標準偏差が 0 の特徴量の削除 deleting_variables = x_train.columns[x_train.std() == 0] x_train = x_train.drop(deleting_variables, axis=1) x_test = x_test.drop(deleting_variables, axis=1) # クロスバリデーションによる木の深さの最適化 cross_validation = KFold(n_splits=fold_number, random_state=9, shuffle=True) # クロスバリデーションの分割の設定 r2cvs = [] # 空の list。木の深さの最大値の候補ごとに、クロスバリデーション後の r2 を入れていきます for max_depth in max_depths: model = DecisionTreeRegressor(max_depth=max_depth, min_samples_leaf=min_samples_leaf, random_state=59) estimated_y_in_cv = cross_val_predict(model, x_train, y_train, cv=cross_validation) r2cvs.append(r2_score(y_train, estimated_y_in_cv)) |
ハイパーパラメータチューニングの学習曲線を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# グラフのサイズの設定 plt.figure(figsize=(6, 4)) scatter = plt.scatter(max_depths, r2cvs, c='blue', alpha=0.7, edgecolors='w', s=80, linewidths=1) # 軸ラベルの設定 plt.xlabel('Maximum Depth of Tree', fontsize=12) plt.ylabel('$r^2$ in Cross-Validation', fontsize=12) # タイトルの設定 plt.title('Optimal Tree Depth in Cross-Validation', fontsize=12) # グリッドラインの追加 plt.grid(True, linestyle='--', alpha=0.6) # グラフの表示 plt.show() optimal_max_depth = max_depths[np.where(r2cvs==np.max(r2cvs))[0][0]] print('最適化された木の深さの最大値 :', optimal_max_depth) |
チューニングされたハイパーパラメータを用いて決定木モデルを構築します。
|
1 2 3 4 5 6 7 |
# モデル構築 model = DecisionTreeRegressor(max_depth=optimal_max_depth, min_samples_leaf=min_samples_leaf, random_state=59) # DT モデルの宣言 model.fit(x_train, y_train) # モデル構築 # トレーニングデータの推定 estimated_y_train = model.predict(x_train) # y の推定 estimated_y_train = pd.DataFrame(estimated_y_train, index=x_train.index, columns=['estimated_y']) |
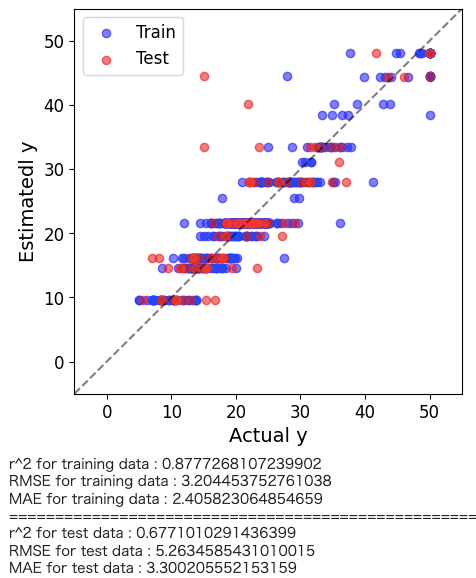
決定木回帰の解析結果がどの程度の予測精度を有しているかを直感的に理解するためにyyプロットを作図します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
plt.figure(figsize=(5,5)) predicte_y_train = model.predict(x_train) predicte_y_test = model.predict(x_test) plt.scatter(y_train, predicte_y_train,color='blue',alpha=0.5,label="Train") plt.scatter(y_test, predicte_y_test,color='red',alpha=0.5,label="Test") plt.plot([-5.,60],[-5,60], 'k--',alpha=0.5) plt.xlim(-5,55) plt.ylim(-5,55) plt.xlabel("Actual y",fontsize=14) plt.ylabel("Estimatedl y",fontsize=14) plt.legend(loc="best") plt.show() # トレーニングデータのr2, RMSE, MAE print('r^2 for training data :', r2_score(y_train, predicte_y_train)) print('RMSE for training data :', mean_squared_error(y_train, predicte_y_train, squared=False)) print('MAE for training data :', mean_absolute_error(y_train, predicte_y_train)) print("==========================================================") # テストデータのr2, RMSE, MAE print('r^2 for test data :', r2_score(y_test, predicte_y_test)) print('RMSE for test data :', mean_squared_error(y_test, predicte_y_test, squared=False)) print('MAE for test data :', mean_absolute_error(y_test, predicte_y_test)) |
決定木の出力
最適化された決定木構造を出力します。
|
1 2 3 4 5 6 |
# ファイルを読み込む with open("tree.dot") as f: dot_graph = f.read() # dotファイルを可視化 graphviz.Source(dot_graph) |
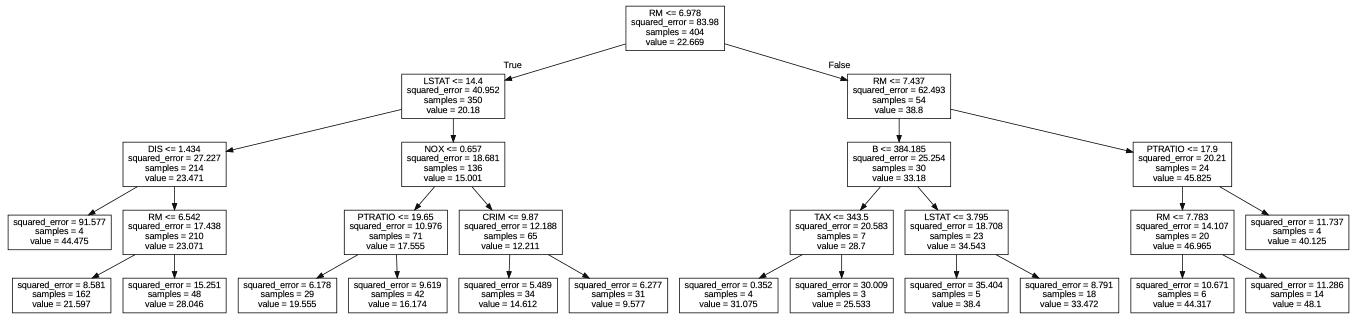
上記のグラフの見方を以下に示します。
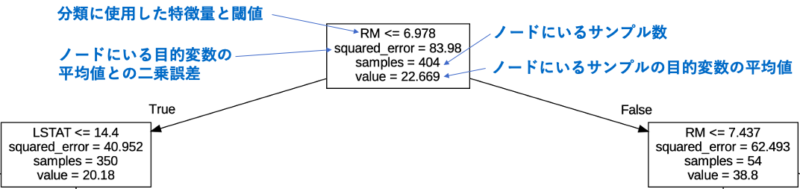
木構造が深く(下にいく)なるにつれて二乗誤差が小さくなっているのがわかります。
この値を指標に決定木モデルが最適化されるように学習を行います。
決定木重要度の出力
決定木では、各ノードでの分割に使われた特徴量から特徴量重要度を計算できます。それにより特定の特徴量がモデルの予測にどれだけ影響を及ぼしているかを数値化します。
重要度は大きいほど重要で、全特徴量の合計が1になるように正規化されます。
特徴量重要度を理解することで、モデルの動作を深く理解し、特徴の選択やモデル改善に役立てることができます。
以下のコードで特徴量重要度を出力します。
|
1 2 3 4 5 6 7 |
importances = model.feature_importances_ # 特徴名と重要度をデータフレームに格納 feature_importances = pd.DataFrame({'Feature': x_train.columns, 'Importance': importances}) # 重要度順にソート feature_importances = feature_importances.sort_values('Importance', ascending=False) # 結果を表示 feature_importances |
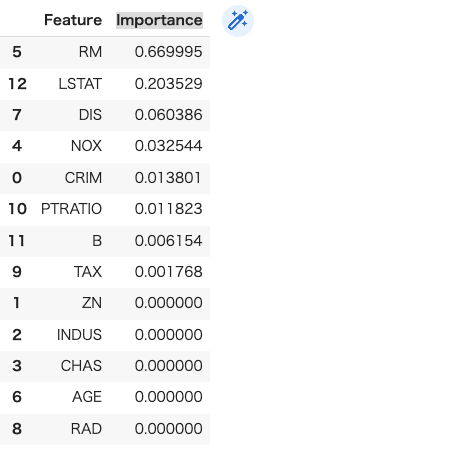
以下のコードで特徴量重要度をグラフ化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
importance = feature_importances["Importance"] # カラム名を取得 column_names = feature_importances["Feature"] # グラフのスタイルを設定 sns.set(style='whitegrid') # プロットのサイズを調整 plt.figure(figsize=(12, 6)) # 係数のバー表示 plt.bar(column_names, importance) # 軸のラベルを設定 plt.xlabel('Feature Names') plt.ylabel('Importance Value') # グリッド線を表示 plt.grid(True) # タイトルを設定 plt.title('Decision Tree Importance') # グラフを表示 plt.show() |
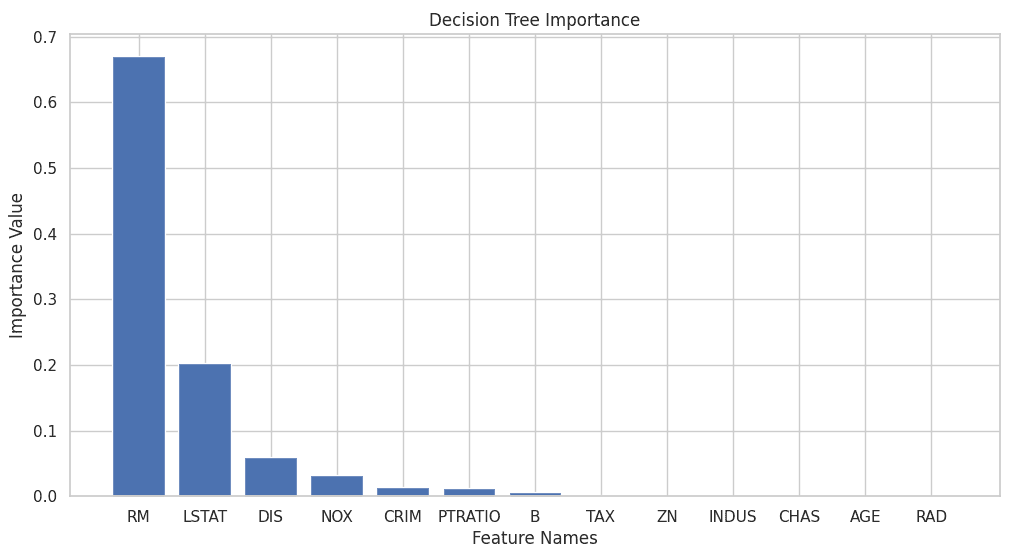
まとめ
今回は、直感的でルールベースのモデルである「決定木回帰分析」について解説しました。
決定木は、データの特徴と目的変数との間の関係を視覚的に捉え、解釈しやすい予測を提供します。また、モデルが意思決定を行う過程を明確に示すことで、特徴の重要性や予測の根拠を解釈できます。
さらに、非線形の関係性も捉えられるという大きな利点を持っています。
Pythonを使った決定木回帰分析の具体的な実装法やについても紹介しましたので、是非このツールを活用していただけばと思います。



コメント