こんにちは、nissyです。前回は、決定木について解説しました。今回は、決定木の発展形である「ランダムフォレスト」について取り上げます。
ランダムフォレストは、決定木の強力な表現力と解釈可能性を維持しつつ、その欠点(過学習)を補完する優れた手法です。
ランダムフォレストとは?
ランダムフォレストは、弱学習器としての多数の決定木を訓練し、その予測を組み合わせて最終的な予測を生成するアンサンブル学習の一つです。
ランダムフォレストでは、バギングというテクニックが利用されます。バギング(Bootstrap Aggregating)は、元のデータセットからランダムに選び出したデータ(ブートストラップサンプル)を使用して、多数の弱学習器を訓練する手法です。
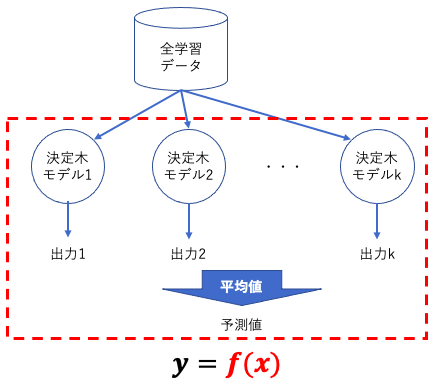
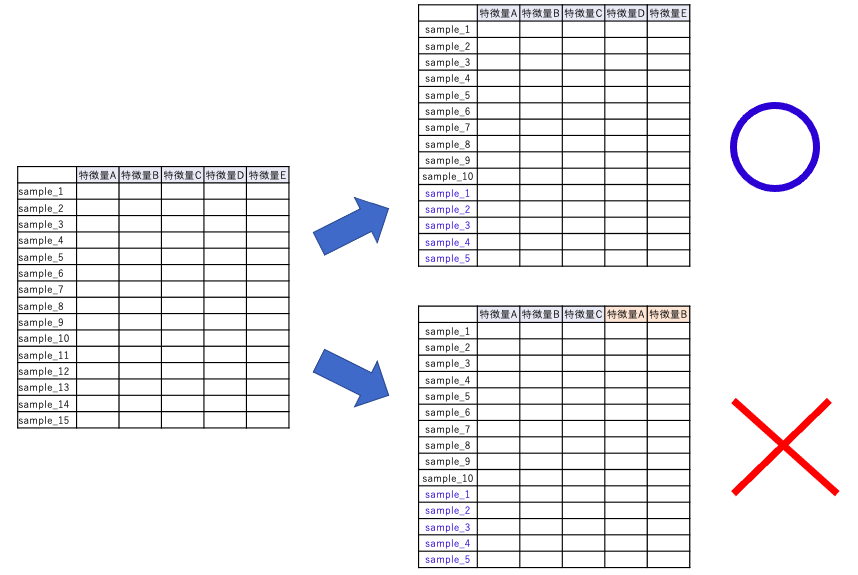
ブートストラップ法とは、元のデータセットから重複を許してランダムにデータを選び出すサンプリング手法を指します。これにより各決定木は異なるデータセットから学習を行い、これがランダムフォレストが過学習を抑制する主要なメカニズムとなります。
また、ランダムフォレストには、Out Of Bag (OOB)という重要な概念があります。ブートストラップサンプリングにより、一部のデータはサンプルされずに”袋”の中に残ることがあり、これをOOBデータと呼びます。
これらのOOBデータを使用して、各決定木の性能を評価することができます。これにより、追加の検証データセットを必要とせずにモデルの性能を推定する効率的な方法を提供します。
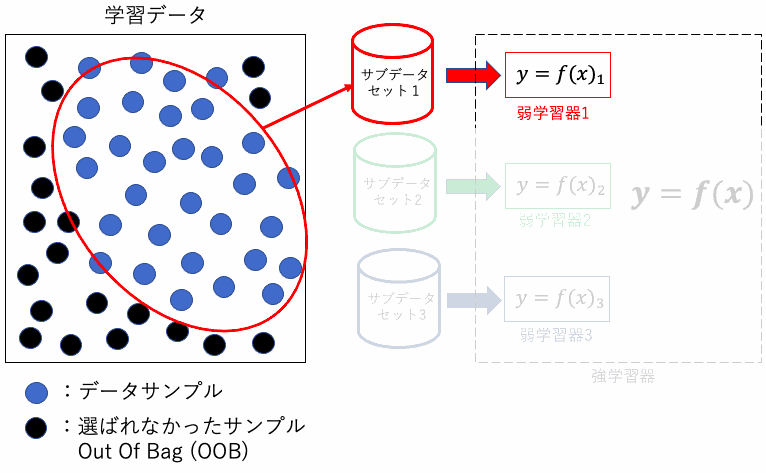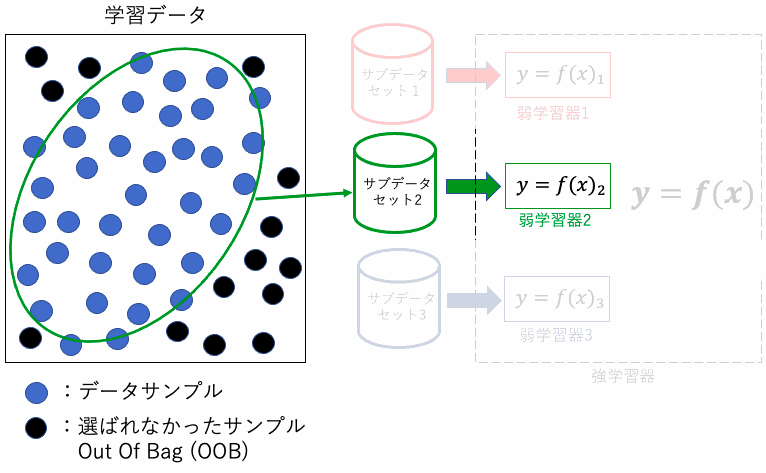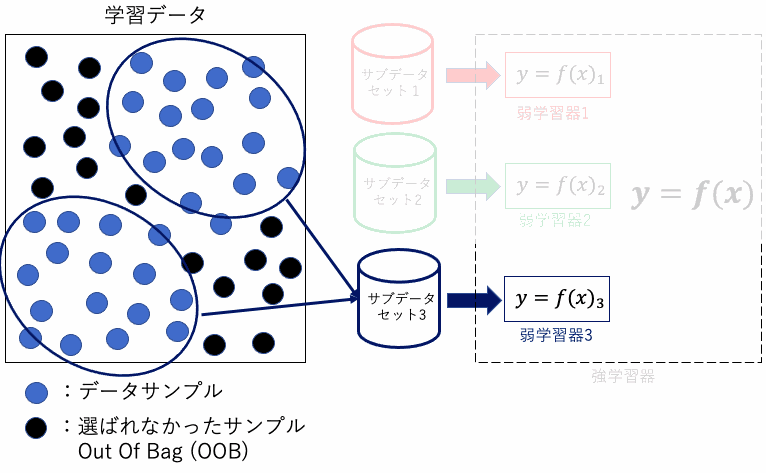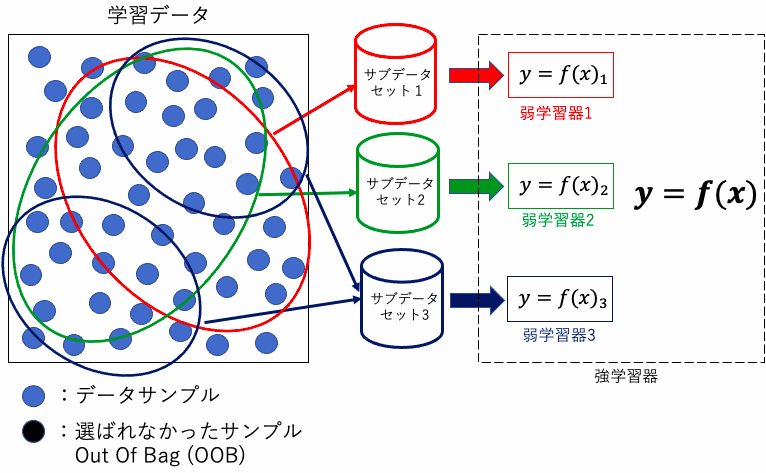
ランダムフォレストはこれらのメカニズムを通じて、データの多様性を保ちつつ、過学習を抑制することができます。
Pythonでのランダムフォレスト実装
今回も「ボストン住宅価格データセット」を用いて「ランダムフォレスト回帰」を行っていきます。
まずは使用するライブラリーをインポートします。
|
1 2 3 4 5 6 7 8 |
import math import matplotlib.pyplot as plt import pandas as pd import numpy as np from sklearn.ensemble import RandomForestRegressor # RF モデルの構築に使用 from sklearn.model_selection import train_test_split from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error import seaborn as sns |
次にボストン住宅価格データセットを用意します。
|
1 2 3 4 5 6 |
data_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data" column_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'PRICE' ] df = pd.read_csv(data_url, header=None, delim_whitespace=True, names=column_names) |
以下のコードでデータを学習データとテストデータに分割します。ランダムフォレストは決定木と同様に、標準化は不要です。
|
1 2 3 4 5 6 |
#================================== # データを学習データとテストデータに分割する #================================== X = df.iloc[:,:-1] y = df["PRICE"] x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) |
学習曲線
ランダムフォレストで設定するハイパーパラメータは以下の4つです。
| max_features | 各決定木で分割に考慮される特徴量の最大数を指定する。特徴量をランダムに選ぶことで、モデルの多様性が増し、過学習を防ぐことができる。max_featuresの値が小さいほど計算速度が速くなるが、バイアスが高くなる(学習不足)。 |
| min_samples_leaf | リーフノード(決定木の末端のノード)に必要な最小のサンプル数。min_samples_leafの値が大きいほどモデルは単純になり、過学習を防ぐことができる(バリアンスが低くなり、バイアスが高くなる)。しかし、値が大きすぎるとモデルが単純すぎてデータのパターンを捉えられなる。 |
| bootstrap | ブートストラップサンプリングを行うかどうかを指定する。ランダムフォレストでは通常、ブートストラップサンプリングを行う。 |
| n_estimators | ランダムフォレストで作成する決定木(弱学習機)の数。n_estimatorsの値が大きいほどモデルのパフォーマンスは向上するが、計算量も増加する。n_estimatorsは経験的に300で安定した値が得られる。 |
以下コードでは各弱学習器の決定木モデルに入力される特徴量の数割合をOOBによって最適化しています。
|
1 2 3 4 5 6 7 8 9 10 11 |
x_variables_rates = np.arange(1, 11, dtype=float) / 10 # 決定木における X の数の割合 number_of_trees = 300 # サブデータセットの数 # OOB を用いた X の数の割合の最適化 r2_oob = [] # 空の list。説明変数の数の割合ごとに、OOB (Out Of Bag) の r2 を入れていきます for x_variables_rate in x_variables_rates: model = RandomForestRegressor(n_estimators=number_of_trees, max_features=int(math.ceil(x_train.shape[1] * x_variables_rate)), oob_score=True) model.fit(x_train, y_train) r2_oob.append(r2_score(y_train, model.oob_prediction_)) |
ハイパーパラメータチューニングの学習曲線を示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# グラフのサイズの設定 plt.figure(figsize=(6, 4)) scatter = plt.scatter(x_variables_rates, r2_oob, c='blue', alpha=0.7, edgecolors='w', s=80, linewidths=1) # 軸ラベルの設定 plt.xlabel('rate of x-variables', fontsize=12) plt.ylabel('$r^2$ in OOB', fontsize=12) # グリッドラインの追加 plt.grid(True, linestyle='--', alpha=0.6) # 目盛りのフォントサイズを設定 plt.tick_params(labelsize=12) # グラフの表示 plt.show() optimal_x_variables_rate = x_variables_rates[np.where(r2_oob == np.max(r2_oob))[0][0]] # r2oob_allが最も大きい X の割合 print('最適化された決定木ごとの X の数 :', int(math.ceil(x_train.shape[1] * optimal_x_variables_rate))) |
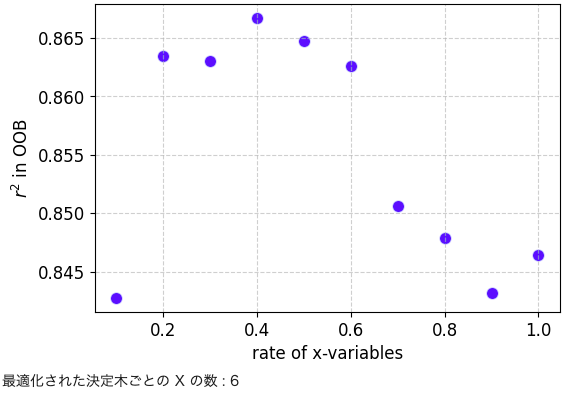
チューニングされたハイパーパラメータを用いてランダムフォレストモデルを構築します。
|
1 2 3 4 5 |
# モデル構築 model = RandomForestRegressor(n_estimators=number_of_trees, max_features=int(math.ceil(x_train.shape[1] * optimal_x_variables_rate)), oob_score=True) # RF モデルの宣言 model.fit(x_train, y_train) # モデル構築 |
ランダムフォレスト回帰の解析結果がどの程度の予測精度を有しているかを直感的に理解するためにyyプロットを作図します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
plt.figure(figsize=(5,5)) predicte_y_train = model.predict(x_train) predicte_y_test = model.predict(x_test) plt.scatter(y_train, predicte_y_train,color='blue',alpha=0.5,label="Train") plt.scatter(y_test, predicte_y_test,color='red',alpha=0.5,label="Test") plt.plot([-5.,60],[-5,60], 'k--',alpha=0.5) plt.xlim(-5,55) plt.ylim(-5,55) plt.xlabel("Actual y",fontsize=14) plt.ylabel("Estimatedl y",fontsize=14) plt.legend(loc="best") plt.show() # トレーニングデータのr2, RMSE, MAE print('r^2 for training data :', r2_score(y_train, predicte_y_train)) print('RMSE for training data :', mean_squared_error(y_train, predicte_y_train, squared=False)) print('MAE for training data :', mean_absolute_error(y_train, predicte_y_train)) print("==========================================================") # テストデータのr2, RMSE, MAE print('r^2 for test data :', r2_score(y_test, predicte_y_test)) print('RMSE for test data :', mean_squared_error(y_test, predicte_y_test, squared=False)) print('MAE for test data :', mean_absolute_error(y_test, predicte_y_test)) |
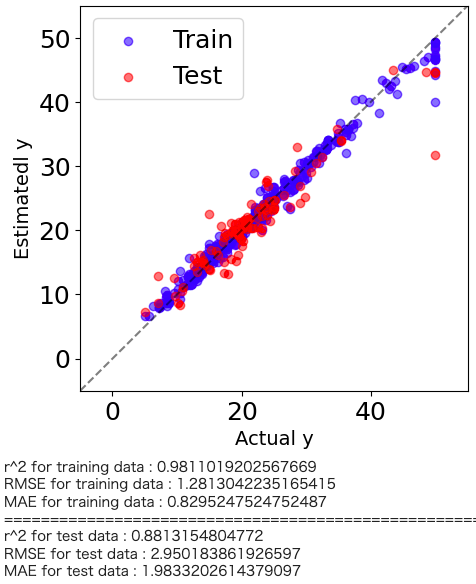
ランダムフォレストの重要度
決定木と同様に、ランダムフォレストも特徴量の重要度を計算することができます。しかしここでの重要度は、すべての決定木にわたって平均化されたものとなります。この特性により、ランダムフォレストは各特徴がモデル全体にとってどれだけ重要であるかを評価するのに非常に役立ちます。
|
1 2 3 |
# 特徴量の重要度 variable_importances = pd.DataFrame(model.feature_importances_, index=x_train.columns, columns=['importances']) # Pandas の DataFrame 型に変換 variable_importances |
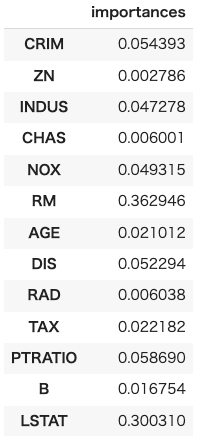
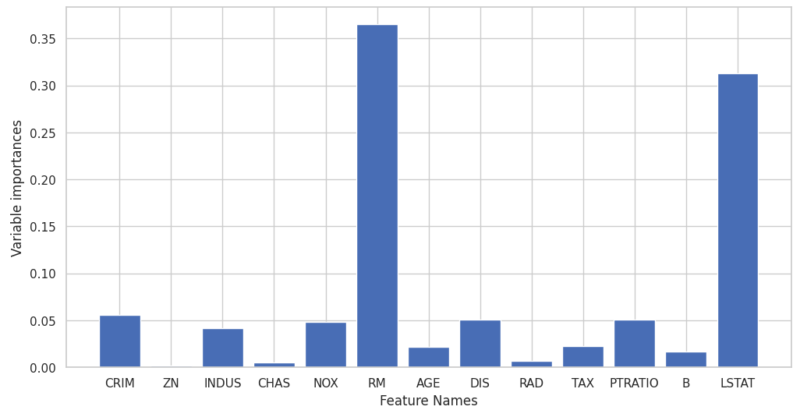
以下のコードで特徴量重要度をグラフ化します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# グラフのスタイルを設定 sns.set(style='whitegrid') # プロットのサイズを調整 plt.figure(figsize=(12, 6)) # 係数のバー表示 plt.bar(variable_importances.index, variable_importances["importances"]) # 軸のラベルを設定 plt.xlabel('Feature Names') plt.ylabel('Variable importances') # x軸のラベルを回転させて表示 # plt.xticks(rotation=90) # グリッド線を表示 plt.grid(True) # タイトルを設定 # plt.title('Variable importances') # グラフを表示 plt.show() |
ランダムフォレストの課題
一方で、ランダムフォレストも完璧な手法ではありません。その一つの課題として、計算コストが挙げられます。
多数の決定木を個別に学習させるため、その分だけ計算量が増えるという欠点があります。
また、ランダムフォレストの予測結果の解釈性は、単一の決定木よりも少し難しくなります。
それぞれの決定木が独立に学習され、その結果が集約されるため、個々の決定に至る過程は透明性を欠く場合があります。
まとめ
今回は、決定木の発展形である「ランダムフォレスト」について解説しました。
ランダムフォレストは、多数の決定木(弱学習器)を訓練し、それらの予測を組み合わせることで最終的な予測値を出力します。これにより、決定木の表現力と解釈可能性は保持しつつ、その欠点である過学習を補う強力な手法です。
Pythonを使ったランダムフォレスト回帰分析の具体的な実装法やについても紹介しましたので、是非このツールを活用していただけばと思います



コメント