こんにちは、nissyです。
本日はランダムフォレストをさらに発展させた「勾配ブースティング」について解説します。。
勾配ブースティングは、決定木やランダムフォレストといった既存の手法を更に強化し、予測精度を大幅に向上させることができるアルゴリズムです。
この記事では、勾配ブースティングの基本的な概念から、その背後にある原理、そして具体的なコードによる実装までを詳しく解説します。
既に決定木やランダムフォレストについての知識を持っている方にとっては、勾配ブースティングはその次のステップとなるでしょう。また、これから機械学習を学び始める方にとっても、勾配ブースティングはその強力さと汎用性から、ぜひ理解しておきたい手法の一つです。
ブースティングとは何か
ブースティングの基本的なアイデアは、複数の弱学習モデル(通常は決定木)を順番に学習し、各モデルが前のモデルの誤りを修正するように学習することです。
つまり、前のモデルが誤って回帰・分類したサンプルに対して、次のモデルは重点的に学習することで、全体としてより正確な予測を行うことを目指します。
具体的には、ブースティングではデータセット内の各サンプルに重みを割り当て、初期モデルを使って予測を行います。その後、誤差を計算し、次のモデルで誤分類されたサンプルに重みを追加します。
これにより、次のモデルはより多くの注意を払ってこれらのサンプルを正確に予測するように学習します。
このプロセスは繰り返され、最終的には複数のモデルの結果を組み合わせることで、より強力な予測モデルが構築されます。
下記イラストは回帰モデルを勾配ブースティングで構築している様子を示しています。赤点のサンプル(モデルが誤ったサンプル)に対して重みを割り当て、優先的に正解するように学習している様子がわかると思います。
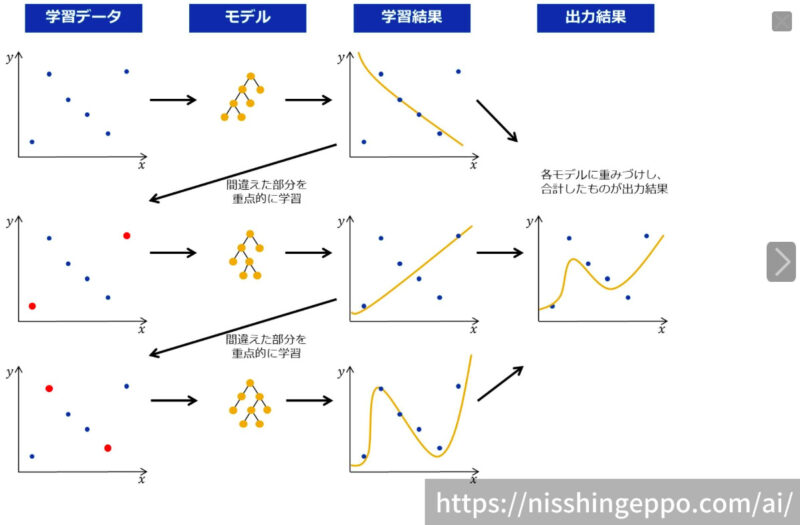
勾配ブースティングの原理
勾配ブースティングはモデルの学習において勾配降下法を活用する手法です。
勾配降下法は、誤差を最小化するためにパラメータを更新する際に勾配(誤差関数の微分)の情報を利用します。
勾配ブースティングでは、弱学習器(通常は決定木)を順番に学習していきます。
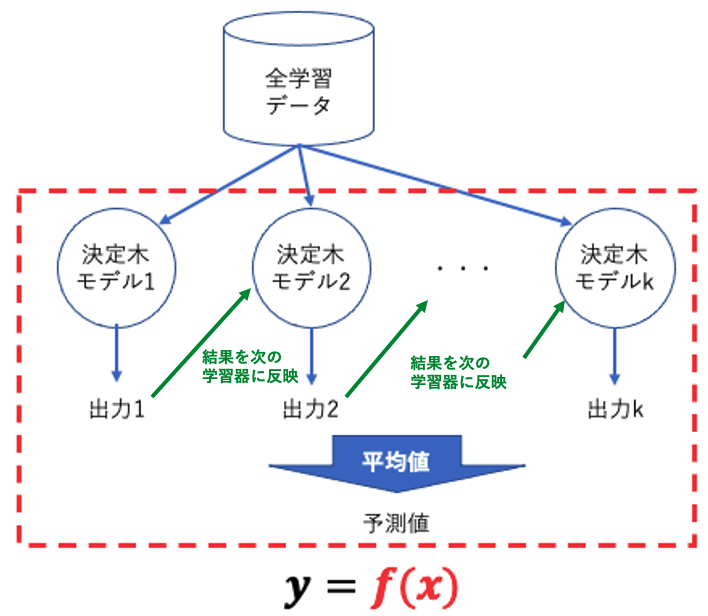
最初のモデルは初期値として与えられ、残差(目標値とモデルの予測値との誤差)を求めます。次に、この残差に対して、新たなモデルを学習させます。
しかし、通常のブースティングとは異なり、新たなモデルの予測値が直接的な目標ではなく、残差を予測するように学習します。
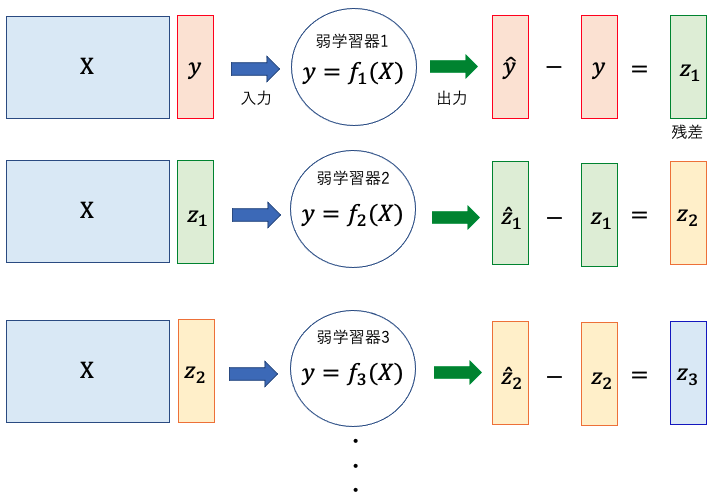
勾配ブースティングでは、各モデルの学習時に勾配(誤差関数の微分)を計算し、残差を最小化するようにパラメータを調整します。
勾配ブースティングではi 回目における二乗平均誤差を損失とし、微分したモデルに学習率ηを掛けた値でモデルを更新します。
\[ L_i =\frac{1}{N}\sum(y^{(i)} – \hat{y}^{(i)})^2\]
\[\hat{y}^{(i+1)} = \hat{y}^{(i)} + \eta\frac{\partial L_i}{\partial y} = \hat{y}^{(i)} +2\eta\sum(y^{(i)} – \hat{y}^{(i)})\]
学習率ηは0〜1の値を取ることができ、値が小さいほど精度は良くなるが、その分計算に時間を要します。
XGBoostとは
XGBoost(eXtreme Gradient Boosting)は勾配ブースティングを活用した高性能な機械学習フレームワークで、競技プログラミングやKaggleなどのデータ分析コンペでも人気の高いアルゴリズムです。
XGBoostは、予測モデルの性能を改善するために、正則化手法を組み込んでいます。
XGBoostは以下の誤差関数を最小化するように学習を行います。
\[ L = \sum_{i} (y^{(i)} , \hat{y}^{(i)}) + \sum_{k} \omega(f_k) \]
\[ \omega(f) = \gamma T + \frac{1}{2} \lambda \|w\|^2 \]
Tは最終ノード(決定木の葉)の数、wは全ての葉ノードの値(葉ノードのサンプルのyの平均値)が格納されたベクトル、決定木の最終てぉな予測値、λとγはハイパーパラメータです。
XGBoostは上記の正則化項を導入することでノード数を小さくしすることで木が複雑になる(オーバーフィッティング)ことを避けています。
それ以外にもXGBoostは、多くの優れた機能を提供しています。例えば、欠損値の処理への頑健性、ランダムフォレストのように特徴量重要度の推定など、モデルの解釈性を高めるためのツールも備えています。
XGBoostのハイパーパラメータ
XGBoostの性能を最大限に引き出すためのハイパーパラメータについて説明します。
Pythonではハイパーパラメータチューニングのためのライブラリがいくつか完備されています。以下に主なライブラリとそれらのメリット・デメリットについてまとめます。
| Scikit-Optimize | KerasTuner | Optuna | |
| メリット | Scikit-learnとの高い互換性があり、Scikit-learnのAPIを知っていれば容易に使用することができる。 | KerasやTensorFlowとの高い互換性があり、深層学習のハイパーパラメータチューニングに特化している。 | 並列化や分散処理が可能で、大規模な最適化タスクにも対応できる。 Scikit-learnやPyTorch、TensorFlow、Kerasなど、多くのライブラリとの互換性がある。 |
| デメリット | 他のライブラリに比べて機能が少なく、特に深層学習のハイパーパラメータチューニングには不向き。 | KerasやTensorFlow以外のフレームワークとの互換性が低い。 | 特定のフレームワークに特化した機能は少ない。 |
XGBoostの主なハイパーパラメータをまとめます。
| 項目 | 説明 | 数値型 | 探索範囲 | 抽出分布 |
| n_estimator | イテレーションの回数 | 整数 | 10~5,000 | |
| learning_rate | 勾配降下法のステップサイズ。通常は対数一様分布からサンプリングされる。 | 実数 | 0.01~1.0 | 対数一様分布 |
| min_child_weight | 分岐に必要な最小インスタンス数またはウェイトの総和。 | 整数 | 1~10 | 一様分布 |
| max_depth | 特徴量に基づく分岐の最大数。 | 整数 | 1~50 | |
| max_delta_step | 各木の重みの推定値において、推測された重みの変化の最大値。 | 整数 | 0~20 | |
| subsample | 訓練に使うサンプルのサブサンプリングの比率 | 実数 | 0.1~1.0 | |
| colsample_bytree | 特徴量のサンプリングの比率を表す | 実数 | 0.1~1.0 | |
| colsample_bylevel | 決定着の深さレベルでの特徴量のサブサンプリングの比率 | 実数 | 0.1~1.0 | |
| reg_lambda | L2正則化を制御する実数 | 実数 | le-9~100.0 | 対数一様分布 |
| reg_alpha | L1正則化を制御する実数 | 実数 | le-9~100.0 | 対数一様分布 |
| gamma | 決定着を分割するための損失関数の減少の下限 | 実数 | le-9~0.5 | 対数一様分布 |
| scale_pos_weight | 陰性クラス(1)に対する要請クラスの重み比率。 | 実数 | le-6~500.0 | 対数一様分布 |
これまで使用したアルゴリズムと比べて非常にハイパーパラメータが多い事がわかります。
PythonでXGBoost実装
今回も「ボストン住宅価格データセット」を用いて「ランダムフォレスト回帰」を行っていきます。
まずは使用するライブラリーをインポートします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import numpy as np import pandas as pd from time import time import pprint import joblib from functools import partial import warnings from xgboost import XGBRegressor from sklearn.model_selection import StratifiedKFold from sklearn.model_selection import KFold from skopt import BayesSearchCV from skopt.callbacks import DeadlineStopper, DeltaYStopper from skopt.space import Real, Categorical, Integer import seaborn as sns from matplotlib import pyplot as plt from sklearn.model_selection import train_test_split from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error |
次にボストン住宅価格データセットを用意します。
|
1 2 3 4 5 6 |
data_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data" column_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'PRICE' ] df = pd.read_csv(data_url, header=None, delim_whitespace=True, names=column_names) |
以下のコードでデータを学習データとテストデータに分割します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#================================== # データを学習データとテストデータに分割する #================================== X = df.iloc[:,:-1] y = df["PRICE"] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # ======================== # データセットの標準化 #======================== autscaled_X_train = (X_train - X_train.mean())/X_train.std() autscaled_X_test = (X_test - X_train.mean())/X_train.std() autscaled_y_train = (y_train - y_train.mean())/y_train.std() autscaled_y_test = (y_test - y_train.mean())/y_train.std() |
ベイズ最適化によるパラメータチューニング
ハイパーパラメータチューニングの結果を出力する関数を設定します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
def report_perf(optimizer, X, y, title="model", callbacks=None): start = time() if callbacks is not None: optimizer.fit(X, y, callback=callbacks) else: optimizer.fit(X, y) d=pd.DataFrame(optimizer.cv_results_) best_score = optimizer.best_score_ best_score_std = d.iloc[optimizer.best_index_].std_test_score best_params = optimizer.best_params_ print((title + " took %.2f seconds, candidates checked: %d, best CV score: %.3f " + u"\u00B1"+" %.3f") % (time() - start, len(optimizer.cv_results_['params']), best_score, best_score_std)) print('Best parameters:') pprint.pprint(best_params) print() return best_params |
XGBoostのモデルを定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#================================== #XGBoost モデルの定義 #================================== #スコア関数を設定 scoring = make_scorer(partial(mean_squared_error, squared=False), greater_is_better=False) #検証戦略を設定 kf = KFold(n_splits=5, shuffle=True, random_state=0) #基本的な回帰モデルを設定 reg = XGBRegressor(boosting_type="gbdt", metric="rmse",n_jobs=1, verbose=-1, random_state=0) |
ベイズ最適化でデューニングするハイパーパラメータを指示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
#================================== # XGBoost ハイパーパラメータ #================================== search_spaces = { 'n_estimators': Integer(10, 5000), 'learning_rate': Real(0.01, 1.0, 'log-uniform'), 'reg_lambda': Real(1e-9, 100.0, 'log-uniform'), 'reg_alpha': Real(1e-9, 100.0, 'log-uniform'), 'subsample': Real(0.01, 1.0, 'uniform'), 'colsample_bytree': Real(0.01, 1.0, 'uniform'), 'colsample_bylevel': Real(0.01, 1.0, 'uniform'), 'max_depth': Integer(1, 50), 'min_child_weight': Integer(1, 10, 'uniform'), 'gamma': Real(1e-9, 0.5, 'log-uniform') } |
ハイパーパラメータチューニングの条件を指示します。今回はScikit-Optimizeを使用してハイパーパラメータチューニングを実施していきます。
|
1 2 3 4 5 6 7 8 9 10 11 |
opt = BayesSearchCV(estimator=reg, search_spaces=search_spaces, scoring=scoring, cv=kf, n_iter=60, n_jobs=-1, iid=False, return_train_score=False, refit=False, optimizer_kwargs={'base_estimator': 'GP'}, random_state=0) |
以下のコードを走らせるとベイズ最適化によるハイパーパラメータチューニングが開始されます。
|
1 2 3 4 5 |
overdone_control = DeltaYStopper(delta=0.0001) time_limit_control = DeadlineStopper(total_time=60 * 60 *6) best_params = report_perf(opt, autscaled_X_train, autscaled_y_train,'XGBoost_regression', callbacks=[overdone_control, time_limit_control]) |
計算の結果、以下のようなハイパーパラメータの値を返してくれました。Google Colaboratryで計算させたのですが、約8分ほど時間がかかりました。

上記のハイパーパラメータを使ってXGBoostを学習させます。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#======================================= # XGBoostモデルを最適なパラメータで訓練 #======================================= model = XGBRegressor(**best_params) model.fit(autscaled_X_train, autscaled_y_train) #======================================= # テストデータの予測 #======================================= predicte_y_train = model.predict(autscaled_X_train)*y_train.std()+y_train.mean() predicte_y_test = model.predict(autscaled_X_test)*y_train.std()+y_train.mean() |
結果を出力します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
plt.figure(figsize=(5,5)) plt.scatter(y_train, predicte_y_train,color='blue',alpha=0.5,label="Train") plt.scatter(y_test, predicte_y_test,color='red',alpha=0.5,label="Test") plt.plot([-5.,60],[-5,60], 'k--',alpha=0.5) plt.xlim(-5,55) plt.ylim(-5,55) plt.xlabel("Actual y",fontsize=14) plt.ylabel("Estimatedl y",fontsize=14) plt.legend(loc="best") plt.show() # トレーニングデータのr2, RMSE, MAE print('r^2 for training data :', r2_score(y_train, predicte_y_train)) print('RMSE for training data :', mean_squared_error(y_train, predicte_y_train, squared=False)) print('MAE for training data :', mean_absolute_error(y_train, predicte_y_train)) print("==========================================================") # テストデータのr2, RMSE, MAE print('r^2 for test data :', r2_score(y_test, predicte_y_test)) print('RMSE for test data :', mean_squared_error(y_test, predicte_y_test, squared=False)) print('MAE for test data :', mean_absolute_error(y_test, predicte_y_test)) |
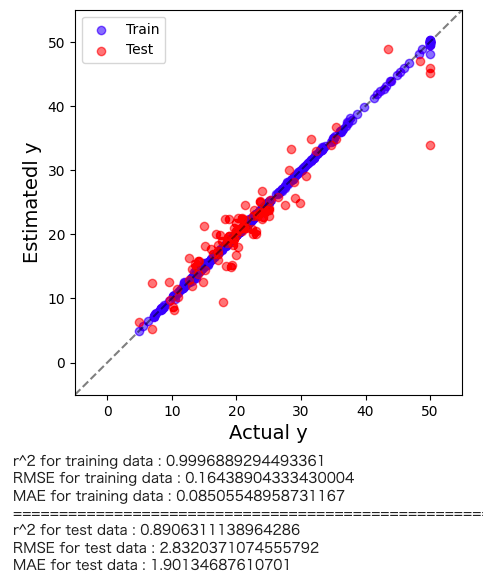
高い精度で予測できている事が確認できます。
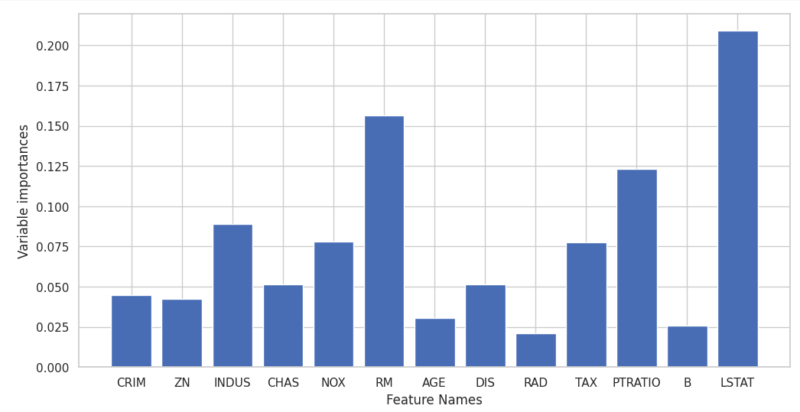
ランダムフォレストと同様に、学習に使ったデータの特徴量重要度を出力します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# グラフのスタイルを設定 sns.set(style='whitegrid') # プロットのサイズを調整 plt.figure(figsize=(12, 6)) # 係数のバー表示 plt.bar(variable_importances.index, variable_importances["importances"]) # 軸のラベルを設定 plt.xlabel('Feature Names') plt.ylabel('Variable importances') # x軸のラベルを回転させて表示 # plt.xticks(rotation=90) # グリッド線を表示 plt.grid(True) # タイトルを設定 # plt.title('Variable importances') # グラフを表示 plt.show() |
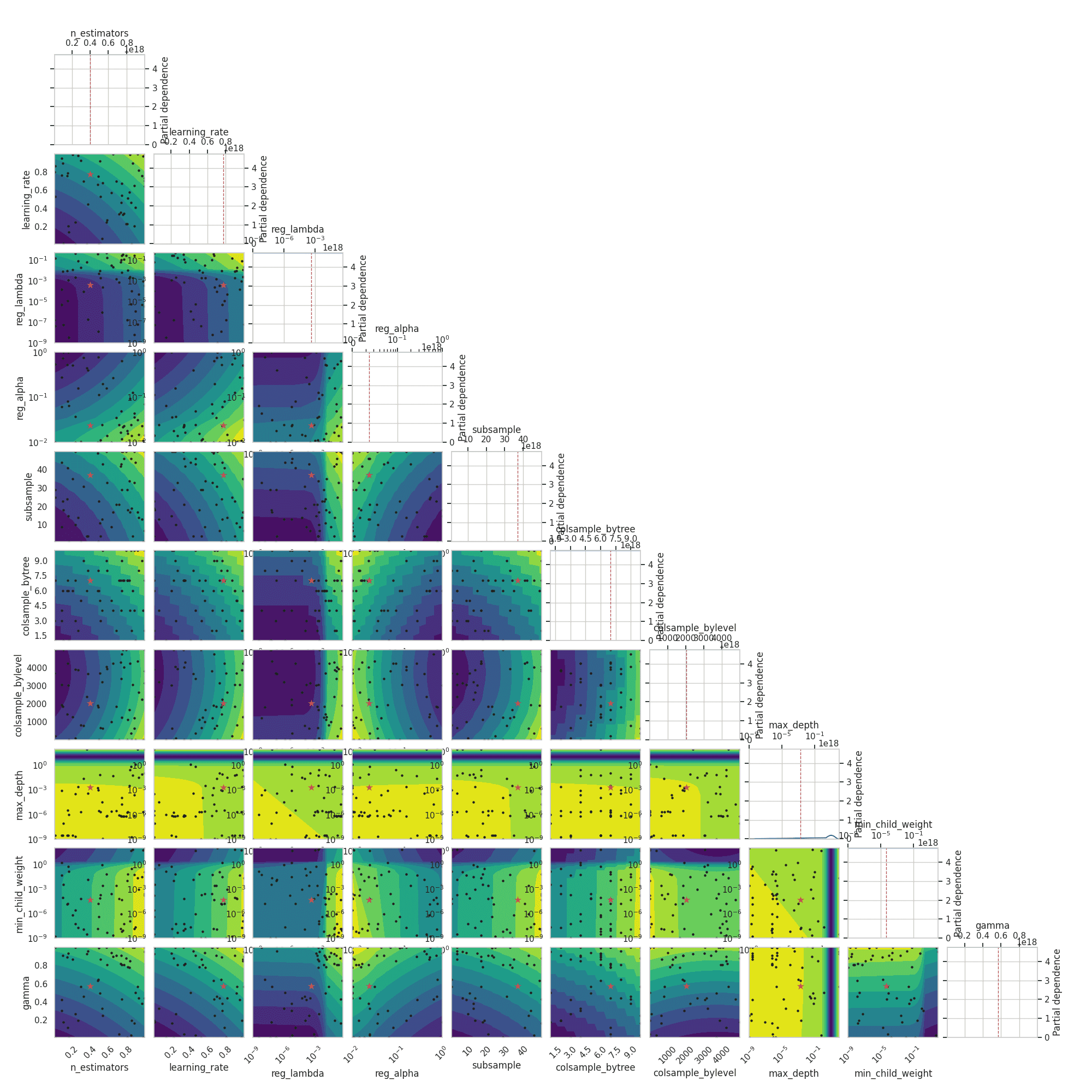
また、ベイズ最適化によるハイパーパラメータチューニングの様子も可視化する事ができます。
|
1 2 3 4 5 6 7 |
from skopt.plots import plot_objective, plot_histogram dimensions= ['n_estimators','learning_rate','reg_lambda','reg_alpha','subsample','colsample_bytree','colsample_bylevel','max_depth','min_child_weight','gamma'] _ = plot_objective(opt.optimizer_results_[0], dimensions=dimensions, n_minimum_search=int(1e8)) plt.show() |
デフォルトのハイパーパラメータ値での予測
XGBoostはハイパーパラメータが多く、チューニングも非常に重要にはなるのですが、デフォルト値のまま学習させても高い予測精度を示します。実際に確認してみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#======================================= # XGBoostモデルをデフォルト値で再訓練 #======================================= model = XGBRegressor() model.fit(autscaled_X_train, autscaled_y_train) #======================================= # テストデータの予測 #======================================= predicte_y_train = model.predict(autscaled_X_train)*y_train.std()+y_train.mean() predicte_y_test = model.predict(autscaled_X_test)*y_train.std()+y_train.mean() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
plt.figure(figsize=(5,5)) plt.scatter(y_train, predicte_y_train,color='blue',alpha=0.5,label="Train") plt.scatter(y_test, predicte_y_test,color='red',alpha=0.5,label="Test") plt.plot([-5.,60],[-5,60], 'k--',alpha=0.5) plt.xlim(-5,55) plt.ylim(-5,55) plt.xlabel("Actual y",fontsize=14) plt.ylabel("Estimatedl y",fontsize=14) plt.legend(loc="best") plt.show() # トレーニングデータのr2, RMSE, MAE print('r^2 for training data :', r2_score(y_train, predicte_y_train)) print('RMSE for training data :', mean_squared_error(y_train, predicte_y_train, squared=False)) print('MAE for training data :', mean_absolute_error(y_train, predicte_y_train)) print("==========================================================") # テストデータのr2, RMSE, MAE print('r^2 for test data :', r2_score(y_test, predicte_y_test)) print('RMSE for test data :', mean_squared_error(y_test, predicte_y_test, squared=False)) print('MAE for test data :', mean_absolute_error(y_test, predicte_y_test)) |
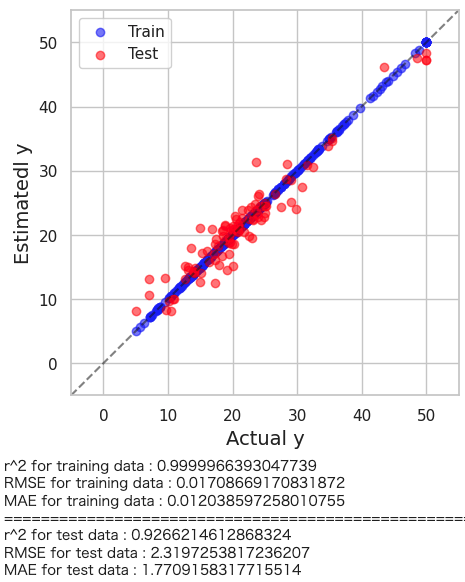
今回はデフォルト値で学習させた方が高い予測精度を示す結果となりました。
解くべき問題にもよりますが、まずはデフォルトのハイパーパラメータでXGBoostを実装してみるのもアリかもしれません。
まとめ
今回は勾配ブースティングを活用した機械学習アルゴリズムについて解説しました。ブースティングは、弱学習モデルを組み合わせて強力な予測モデルを構築する手法であり、XGBoostはその中でも特に優れた性能を持っています。
勾配ブースティングの原理を最大限に活用し、XGBoostは高速かつ高性能なモデルの構築を実現します。逐次的な学習と誤差の最小化を行いながら、複数のモデルを組み合わせることで、予測性能を向上させます。
XGBoostは、さまざまな機械学習タスクに適用可能であり、特に構造化データや高次元データにおいて優れた結果を示します。また、正則化の手法を組み込んでおり、過学習を抑制しモデルの汎化性能を向上させます。
Pythonを使ったXGBoostの実装も容易であり、ライブラリのインストールやデータの準備、モデルの学習・予測までの一連の手順をコード例と共に解説しました。
XBoostはハイパーパラメータが多く、チューニングも非常に重要ですが、デフォルト値でも十分に高い予測精度を示す事が多いです。解くべき問題にもよりますが、まずはデフォルトのハイパーパラメータでXGBoostを実装してみるのことをお勧めします。



コメント