こんにちはnissyです
前回のブログでTanimoto-kernel 搭載 サポートベクター回帰を紹介させてもらいました。
この手法について勉強していた時にふと考えが浮かんだのです!
「これってベイズ最適化に応用出来んじゃね?」
ということで、Tanimoto-kernelを使ったベイズ最適化の手法について解説して行きます!
大変申し訳ございませんが、ベイズ最適化については既知の提で書かせていただきましたm(_ _)m
ベイズ最適化について興味のある方は、こちらの書籍がおすすめです。
|
|
Tanimoto-kernel 搭載 ガウス過程回帰
やり方は非常にシンプルで、Tanimoto-kernelを搭載したガウス過程回帰でモデリングを行います。
それでは早速ライブラリを読み込みます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import os import pandas as pd import numpy as np import matplotlib.figure as figure import matplotlib.pyplot as plt from rdkit import Chem from rdkit.Chem import AllChem, Draw from sklearn.model_selection import train_test_split,GridSearchCV from sklearn.metrics import r2_score, mean_absolute_error from dcekit.variable_selection import search_high_rate_of_same_values, search_highly_correlated_variables import glob from sklearn.metrics.pairwise import pairwise_distances from sklearn.base import BaseEstimator, RegressorMixin, ClassifierMixin from sklearn.metrics.pairwise import pairwise_kernels from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error from sklearn.metrics import jaccard_score from sklearn.gaussian_process import GaussianProcessRegressor # GPR モデル構築に使用 from sklearn.gaussian_process.kernels import Kernel from sklearn.model_selection import KFold # 内側の CV の分割の設定に使用 from sklearn.model_selection import GridSearchCV # グリッドサーチに使用 |
データセットの準備
SMILESのフィンガープリントに変換するまでは、過去のブログで紹介してるのでそちらも参照してください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
#========================== # 学習データのサンプル数が50になるように調整 #========================== df = pd.read_csv('SMILES_logS_データセット.csv') df_train, df_test= train_test_split(df, train_size=0.039, random_state=42) #=========== # 目的変数の中心化 標準化をすると学習精度が悪くなる #=========== y_name = "logS" train_y = df_train[y_name] train_y_ave = train_y.mean() centered_train_y = train_y - train_y_ave #================================ # SMILES⇒ECFP4への変換 #================================ radius= 2 bit =2048 mols_list = [Chem.MolFromSmiles(smiles) for smiles in df_train["SMILES"]] ECFP = [AllChem.GetMorganFingerprintAsBitVect(mol, radius,bit) for mol in mols_list] df_X = pd.DataFrame(np.array(ECFP, int)) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
class TanimotoKernel(Kernel): def __init__(self): pass def __call__(self, X, Y=None): """ カスタムカーネル関数。ジャッカード類似度行列を計算する。 Parameters: X (pd.DataFrame or np.ndarray): サンプルデータ Y (pd.DataFrame or np.ndarray, optional): サンプルデータ。指定しない場合はXを使用します。 Returns: np.ndarray: ジャッカード類似度行列 """ if isinstance(X, pd.DataFrame): X = X.values if Y is None: Y = X elif isinstance(Y, pd.DataFrame): Y = Y.values num_samples_X = X.shape[0] num_samples_Y = Y.shape[0] similarity_matrix = np.zeros((num_samples_X, num_samples_Y)) # ジャッカード類似度の計算 for i in range(num_samples_X): for j in range(num_samples_Y): similarity_matrix[i, j] = jaccard_score(X[i], Y[j]) return similarity_matrix def diag(self, X): # 対角成分を返す(自己相似度は常に1と仮定) return np.ones(X.shape[0]) def is_stationary(self): # このカーネルは「定常」ではない(時間や空間の変動に依存するため) return False |
ダブルクロスバリデーションで予測精度を確認
Tanimoto-kernelを搭載したガウス過程回帰での予測精度を確認したく、ダブルクロスバリデーション(DCV)を用いて予測精度を評価します。
ダブルクロスバリデーションの詳細については論文を参照ください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
estimated_y_in_outer_cv = centered_train_y.copy() # 外側の CV による y の推定結果を格納する変数 estimated_y_in_outer_cv outer_fold_number = 5 # 外側の CV における fold 数 fold_number = 4 # 内側の CV における fold 数 indexes = [] # fold の番号を格納する変数 for sample_number in range(df_X.shape[0]): indexes.append(sample_number % outer_fold_number) np.random.seed(99) # 再現性のため乱数の種を固定 fold_index_in_outer_cv = np.random.permutation(indexes) # シャッフル np.random.seed() # 乱数の種の固定を解除 # 外側の CV for fold_number_in_outer_cv in range(outer_fold_number): tanimoto_kernel = TanimotoKernel() print(fold_number_in_outer_cv + 1, '/', outer_fold_number) # トレーニングデータとテストデータに分割 x_train = df_X.iloc[fold_index_in_outer_cv != fold_number_in_outer_cv, :] y_train = centered_train_y.iloc[fold_index_in_outer_cv != fold_number_in_outer_cv] x_test = df_X.iloc[fold_index_in_outer_cv == fold_number_in_outer_cv, :] # トレーニングデータを用いたモデル構築 model = GaussianProcessRegressor(kernel=tanimoto_kernel, alpha=1e-5) # GPRモデルの宣言 model.fit(x_train, y_train) # SVRモデル構築 # テストデータの推定 estimated_y_test = model.predict(x_test) # テストデータの推定 # estimated_y_test = estimated_y_test * y_train.std(ddof=1) + y_train.mean() #元のスケールに戻す estimated_y_in_outer_cv[fold_index_in_outer_cv==fold_number_in_outer_cv] = estimated_y_test # 推定結果を格納 |
結果を表示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
predicted_train_y = estimated_y_in_outer_cv + train_y_ave plt.figure(figsize=(5,5)) plt.scatter(train_y.values, predicted_train_y , c="blue",alpha=0.5,label="Train") plt.plot([-60,200],[-60,200],"k",linestyle="dashed",linewidth = 0.8) plt.xlim(-10,2) plt.ylim(-10,2) plt.xlabel("Actual y") plt.ylabel("Predicted y") print('r^2(DCV) :', r2_score(train_y.values, predicted_train_y)) print('RMSE(DCV) :', mean_squared_error(train_y.values, predicted_train_y, squared=False)) print('MAE(DCV) :', mean_absolute_error(train_y.values, predicted_train_y)) plt.show() |
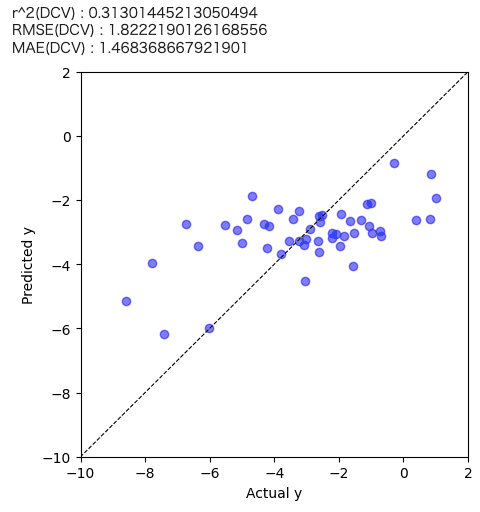
予測精度が高いとは言い難い結果でした。
Tanimoto-kernel搭載ガウス過程回帰のモデリング
それでは実際にTanimoto-kernelを搭載したガウス過程回帰を実装して行きましょう!!
|
1 2 3 4 |
# カスタムカーネルをGaussianProcessRegressorで使用 tanimoto_kernel = TanimotoKernel() model = GaussianProcessRegressor(kernel=tanimoto_kernel, alpha=1e-5) model.fit(df_X.values, centered_train_y) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
predicted_y = model.predict(df_X.values) + train_y_ave plt.figure(figsize=(5,5)) plt.scatter(train_y.values, predicted_y , c="blue",alpha=0.5,label="Train") plt.plot([-60,200],[-60,200],"k",linestyle="dashed",linewidth = 0.8) plt.xlim(-10,2) plt.ylim(-10,2) plt.xlabel("Actual y") plt.ylabel("Predicted y") # plt.title(str(y_name) + ", Concentration: " + str(Concentration)) print('r^2 for test data :', r2_score(train_y.values, predicted_y)) print('RMSE for test data :', mean_squared_error(train_y.values, predicted_y, squared=False)) print('MAE for test data :', mean_absolute_error(train_y.values, predicted_y)) plt.show() |
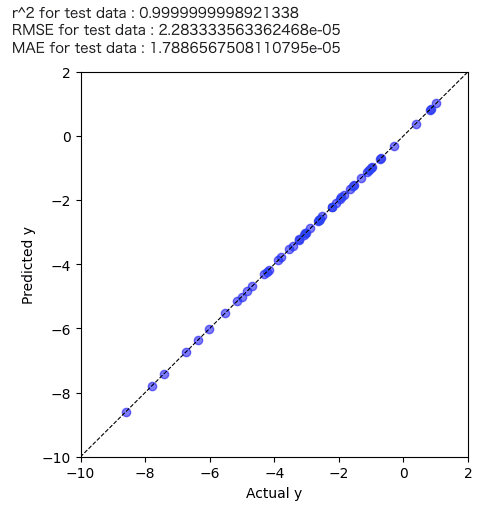
学習はうまくいっているように感じますね。
それでは構築した機械学習モデルを使って、事前にテストサンプルとして取り分けてた1240サンプルの予測平均値と標準偏差を出力してみましょう。まずはテストサンプルのSMILESをフィンガープリントに変換するまでを実施します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
df_candidate = df_test y_test = df_test[y_name] df_candidate = df_candidate.drop(columns=y_name) #========================== # 使えないSMILESを仕分け #========================== mols_list = [] invalid_smiles = pd.DataFrame(columns=["SMILES"]) # 列名を設定してデータフレームを初期化 for smiles in df_candidate["SMILES"]: mol = Chem.MolFromSmiles(smiles) if mol is not None: mols_list.append(mol) else: # エラーが発生したSMILESをデータフレームに追加 invalid_smiles = pd.concat([invalid_smiles, pd.DataFrame({"SMILES": [smiles]})], ignore_index=True) # invalid_smilesのSMILES列をリストに変換 invalid_smiles_list = invalid_smiles["SMILES"].tolist() # df_candidateからinvalid_smiles_listに含まれるSMILESを除外 filtered_df = df_candidate[~df_candidate["SMILES"].isin(invalid_smiles_list)] filtered_df = filtered_df.reset_index().drop(columns = "index") # 指定した半径とビット数を使ってECFPを生成 mols_list = [Chem.MolFromSmiles(smiles) for smiles in filtered_df["SMILES"]] ECFP = [AllChem.GetMorganFingerprintAsBitVect(mol, radius,bit) for mol in mols_list] df_X_candidate = pd.DataFrame(np.array(ECFP, int)) つ |
続いてテストサンプルにたいして目的変数の予測値を出力します。
|
1 2 3 4 5 6 7 8 |
predicted_candidate = pd.DataFrame(model.predict(df_X_candidate.values,return_std=True)) predicted_candidate = predicted_candidate.T predicted_candidate.columns=["Average","STD"] predicted_candidate["Average"] = predicted_candidate["Average"] + train_y_ave df_sum_of_candidate = pd.concat([filtered_df,predicted_candidate],axis=1) df_sum_of_candidate |
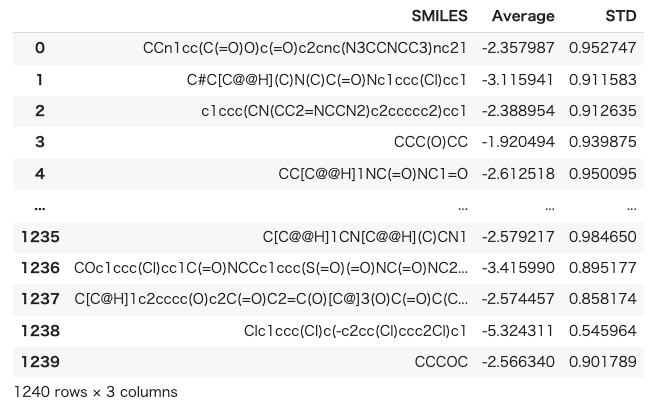
この結果を標準偏差で降順に昇順ソートし、可視化してみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
#======================= # 標準偏差順にソート #======================= df_sum_of_candidate = df_sum_of_candidate.sort_values(by='STD', ascending=True) df_sum_of_candidate = df_sum_of_candidate.reset_index() plt.figure(figsize=(20, 6)) plt.errorbar(df_sum_of_candidate.index, df_sum_of_candidate['Average'], yerr=df_sum_of_candidate['STD'], fmt='.', capsize=5, capthick=2,alpha=0.3) plt.plot(df_sum_of_candidate.index, df_sum_of_candidate['Average'],marker="o") plt.axhline(y=train_y_ave, color='red', linestyle='--', label='Average of train_y') # グラフの装飾 # plt.title('Average with Error Bars (STD)', fontsize=14) # plt.xlabel('Name', fontsize=12) plt.ylabel(y_name, fontsize=12) plt.grid(True) plt.legend() plt.show() |
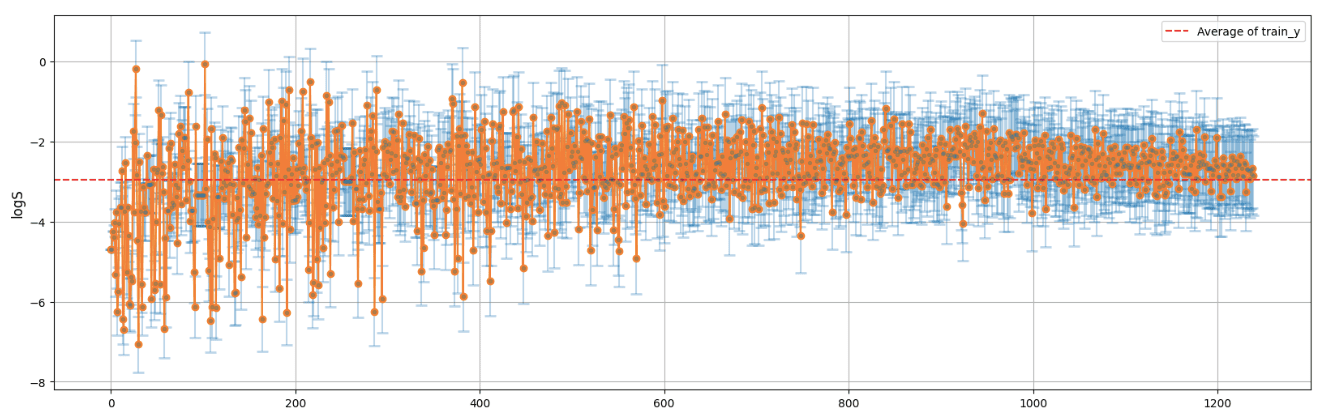
右に行くほど標準偏差が大きくなるように並び替えています。
グラフの結果より、不確実性が高くなるほど予測値は学習データの平均値(グラフ赤点線)に収束していってるようにも見えますね。これはガウス過程回帰の持つ性質でもあるので、まぁいい感じなのかなと。
この予測結果を用いて獲得関数を算出し、次の実験計画を行うことでTanimoto-kernelを使ったベイズ最適化を実施することができます!
これは私自身実際の実験に応用したことが無いので効果は検証できていませんが、興味はありますね。
実際にテストデータの実測値と予測値の関係も確認してみました。
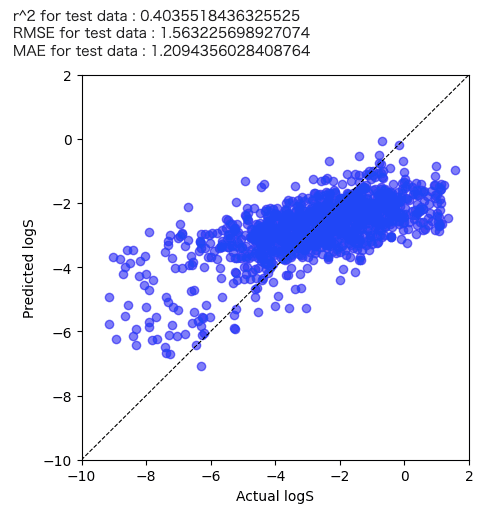
まぁ、50サンプルで学習した結果なのでこんなものかなと・・・
まとめ
今回はTanimoto-kernelを使ったベイズ最適化を思いついたので紹介してみました!実際に材料開発で応用したこと経験は無いのですが、なんとなく有効な気がしています。
また、何か閃いたら紹介して行きたいと思います。
参考文献
P.Filzmoser, B.Liebmann, K.Varmuza, J.Chemom.,22,160(2009)

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/2eaa35ab.09768959.2eaa35ac.789bf136/?me_id=1213310&item_id=20351134&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F5300%2F9784065235300.jpg%3F_ex%3D240x240&s=240x240&t=picttext)



コメント